Цифра 1 на годик своими руками: мастер-классы, шаблоны, видео
Создание фотозоны или отдельных элементов декора для праздничного фотосета является важной частью подготовки к первому дню рождения любимого малыша. Центральное звено композиции на годик – цифру 1 – возможно сделать своими руками. Большие и маленькие, пестрые и однотонные, плоские и объемные – выбирайте любую единичку. Подробные мастер-классы и подборка самых интересных идей на фото помогут создать настоящий шедевр.
Основа для объемной цифры 1
Для больших поделок на день рождения своими руками идеально подойдет заготовка из пенопласта. Несмотря на внушительные размеры такая цифра получается легкой и устойчивой. Делается также достаточно просто – на кусок пенопласта необходимо нанести шаблон единички или построить схему прямо на материале в соответствии с желаемыми размерами готового изделия. Далее требуется вырезать острым канцелярским ножом единичку по намеченным линиям. Важно обработать, зачистить места срезов и постараться сделать ровные, немного закругленные края.
Даже если вы до этого никогда не делали подобных поделок, и получается не самая идеальная цифра 1 – ничего страшного. Большинство вариантов украшений прекрасно скрывают недочеты.
Другой способ смастерить основу для объемной цифры – воспользоваться картоном. При этом, чем больше будет готовая единичка, тем важнее сделать каркас с полостью внутри. Даже если склеить несколько листов картона вместе, метровая циферка может прогибаться в центре от тяжести украшений, а также получится довольно неустойчивой.
Как сделать объемную единицу из картона пошагово:
- На плотный ровный картон нанести шаблон будущего изделия. Размеры и примеры лекал смотрите ниже.
- Вырезать по начерченным линиям.
- Склеить детали бумажным скотчем.
- Украсить цветной бумагой, тканью, шпагатом или другими материалами.
Придавая цифре 1 форму короба, делать заднюю стенку необязательно. Особенно это актуально для громоздких поделок.
Заднюю сторону все равно не будет видно, а исходных материалов и времени на работу создание единички потребует гораздо меньше. К тому же такое изделие легче, удобнее переносить и транспортировать.
Если единица делается из ткани, то основу желательно изготовить из толстого поролона. Если же хочется набить подушечку холофайбером, то придется сшить сначала наперник. Поделки из фетра вообще не требуют каркаса. Достаточно просто сшить вместе две детали, при желании тонким слоем наполнить холофайбером или ватой. Когда требуется цифра около 50 см и выше, желательно использовать основу из картона, чтобы придать изделию устойчивость.
Чем украсить единичку?
Основная работа позади и основа для циферки готова, остается задекорировать поверхность. Материал можно использовать любой. Главное требование – безопасность для малыша. Должны отсутствовать токсичные вещества, сильнопахнущие элементы, мелкие и острые детали. Аналогичные требования предъявляются также к клею. Допустимо использовать степлер, но только при условии, что ребенок потом не будет играть с поделкой.
Допустимо использовать степлер, но только при условии, что ребенок потом не будет играть с поделкой.
Чем можно украсить декоративную цифру 1:
- гофрированная, крафтовая или цветная бумага;
- бумажные столовые салфетки;
- ткань;
- фетр;
- шпагат;
- нитки;
- помпоны;
- атласные ленты;
- фоамиран;
- воздушные шарики.
Гофрированная бумага
Это один из самых популярных способов украсить единичку. Объяснение простое – не требует особых навыков и умений, материалы доступные, результат получается потрясающий. При этом гофрированную бумагу можно клеить разными способами – вырезать из нее длинные бордюрчики с нарезанным в виде травы (бахрамы) краем, складывать небольшие квадратики или формировать цветы.
Как сделать цифру 1 на годик из гофрированной бумаги:
- Подготовить картонный каркас.
- Из гофробумаги вырезать много цветов.
- С помощью термопистолета наклеить бумажные заготовочки на картон так, чтобы не осталось пустых просветов.
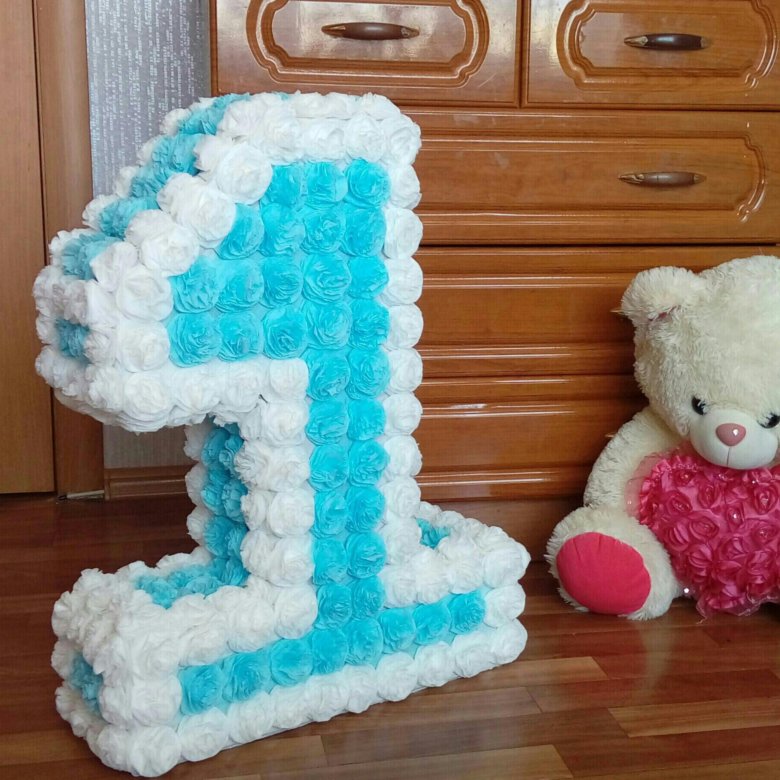
- При желании прикрепить дополнительный декор – бантик-бабочку, корону, мишку, пони, единорога.
Салфетки
Вместо гофрированной бумаги можно использовать обычные бумажные салфетки. При этом чем они тоньше, тем нежнее и красивее получается готовая поделка.
Единичка из салфеток своими руками пошагово:
- Сделать основу из плотного картона.
- Салфетки сложить вместе по несколько штучек (минимум 3-4), вырезать круг.
- В центре собрать в виде бутона и закрепить скрепкой из степлера.
- Края цветочка расправить, распушить.
- Заклеить полученными заготовками всю поверхность цифры.
Ткань, фетр
Единичку на годик своими руками можно сделать из ткани. В результате получится симпатичная подушечка, которой ребенок сможет играть после дня рождения. Первым делом требуется смастерить основу – сшить наперник в виде цифры 1 или единицу вырезать из поролона.
Далее нужно сделать наволочку, чтобы подушечку можно было стирать. Украсить готовое изделие можно по собственному усмотрению. Популярные идеи – это вышитое нитками или нашитое из фетра имя ребенка, всевозможные тканевые аппликации, цветы из лент, органзы или фатина.
Украсить готовое изделие можно по собственному усмотрению. Популярные идеи – это вышитое нитками или нашитое из фетра имя ребенка, всевозможные тканевые аппликации, цветы из лент, органзы или фатина.
Желательно не использовать при украшении бусинок и пуговиц или очень крепко их пришивать.
Из фетра часто делают небольшие циферки в виде игрушек. Для таких изделий делать каркас необязательно, достаточно между двумя основными фетровыми деталями проложить слой холофайбера. Украсить также можно по собственному усмотрению – цветы, игрушки, сказочные персонажи, бабочки.
Шпагат, нитки
Очень интересная идея для небольших единичек размером 30-60 см. Делать объемный каркас необязательно. Достаточно вырезать основу из картона. Далее ее требуется плотно обмотать шпагатом или нитками. Получается поделка в экостиле, которая хорошо впишется в большинство дизайнов фотозоны. Использовать большое количество декора не нужно, для украшения будет достаточно одного-двух аккуратных бантиков или нескольких цветочков.
Атласные ленты
Для начала требуется подготовить основу из картона или пенопласта. При этом ровная поверхность и края очень важны, поскольку это одна из тех поделок, где недочеты будут заметны. Далее заготовку нужно плотно обтянуть широкой атласной лентой. Края закрепить степлером или термоклеем.
Украшения делать из менее широких ленточек, органзы, фетра, бумаги или любых других материалов. Именно на таких циферках красиво смотрится вышивка крупными бусинками или аппликация из пуговиц. Но не стоит забывать о безопасности, поэтому мелкие детали к поделке крепите качественно.
Воздушные шарики
Для создания единички потребуется надуть много воздушных шариков. Крепить их можно на проволочный каркас, что придаст желаемую форму изделию и поможет ее сохранить в дальнейшем. Шарики одинакового размера надувают по шаблону, чтобы поделка выглядела аккуратно и гармонично. Также можно сделать композицию из надутых гелием шаров или собрать аэромозаику.
Примеры единичек из воздушных шариков смотрите на фото:
Шаблоны для изготовления цифры 1 и декора
Чтобы упростить задачу по изготовлению единички, воспользуйтесь готовыми шаблонами и трафаретами.
Полезные фотоматериалы по изготовлению каркаса для объемной цифры 1:
Шаблоны и трафареты для изготовления декоративных элементов из фанеры, картона, бумаги, фетра и прочих материалов:
Фото единичек для девочек
Интересные идеи оформления цифры 1 на годик девочке смотрите в подборке фото:
Фото цифры 1 для мальчика
Как интересно оформить единичку на день рождения мальчика смотрите на фото:
Видео по изготовлению цифры 1
Подробные мастер-классы по изготовлению основы и дальнейшему оформлению единички представлены на видео.
Как сделать каркас из картона:
Цифра 1 из салфеток:
Единичка из гофрированной бумаги:
Композиция из воздушных шариков:
Аэромозаика:
Цифра 1 из ткани и фетра:
Единичку на годик ребенку можно сделать из картона, бумаги, пенопласта, воздушных шариков, ткани, фетра, жгута и прочих материалов. Главное, чтобы данный декоративный элемент не представлял опасности для жизни и здоровья именинника, а также маленьких гостей. Выбирайте интересную идею и воплощайте в жизнь. Красочные и веселые фото будут обеспечены.
Объемная цифра 1 в Украине.
 Цены на Объемная цифра 1 на Prom.ua
Цены на Объемная цифра 1 на Prom.uaРаботает
Свеча Цифра 1 объемная Balloon золото — 1 шт
Доставка из г. Одесса
26 грн
Купить
Интернет — магазин для кондитера
Работает
Часы 3d объемные разборные с римск цифрами серебро до 1м
На складе в г. Киев
Доставка по Украине
565 грн
Купить
Landis
Работает
Часы 3d объемные разборные с цифрами и словами серебро до 1м
На складе в г. Киев
Доставка по Украине
565 грн
Купить
Landis
Работает
Часы 3d объемные разборные с цифрами и словами черные до 1м
На складе в г. Киев
Доставка по Украине
565 грн
Купить
Landis
Работает
Часы 3d объемные разборные со слов и цифр черные до 1м
На складе в г. Киев
Доставка по Украине
565 грн
Купить
Landis
Работает
Часы 3d светящиеся в темноте объемные разборные с 4 цифрами и штрихами до 1м
На складе в г. Киев
Киев
Доставка по Украине
772 грн
Купить
Landis
Работает
Свеча Цифра 0 объемная Balloon золото — 1 шт
Доставка по Украине
26 грн
Купить
Интернет — магазин для кондитера
Работает
Свеча Цифра 3 объемная Balloon золото — 1 шт
Доставка по Украине
26 грн
Купить
Интернет — магазин для кондитера
Работает
Свеча Цифра 4 объемная Balloon золото — 1 шт
Доставка из г. Одесса
26 грн
Купить
Интернет — магазин для кондитера
Работает
Свеча Цифра 6 объемная Balloon золото — 1 шт
Доставка по Украине
26 грн
Купить
Интернет — магазин для кондитера
Работает
Объемная цифра 1 с подсветкой (с лампочками)
Под заказ
Доставка по Украине
1 100 грн
Купить
Serpantin_zp
Работает
Объемная цифра 1 с подсветкой (с лампочками)
Под заказ
Доставка по Украине
1 100 грн
Купить
Serpantin_zp
Работает
Объемная цифра 1 с подсветкой
Под заказ
Доставка по Украине
1 200 грн
Купить
Serpantin_zp
Работает
Объемная цифра 1 с подсветкой RGB
Заканчивается
Доставка по Украине
1 500 грн
Купить
Serpantin_zp
Работает
Аренда Световая объемная цифра 1 с подсветкой (с лампочками)
Услуга
500 грн
hildrenworld
Смотрите также
Работает
Объемная крашеная цифра 1 из пенопласта с блестками (глиттер)
Доставка по Украине
1 190 грн
Купить
Manific Decor
Работает
Объемная цифра 1 2 3 из пенопласта на подставке
Доставка по Украине
1 470 грн
Купить
Manific Decor
Работает
Цифра Буква из Пенопласта 1 шт 90-100 см Объемные Большие Декоративные Декорации на торжество слова на свадьбу
Доставка из г. Одесса
Одесса
380 грн
Купить
НЕВАЛЯШКА — Деревянная Продукция
Работает
Цифра Буква из Пенопласта 1шт 100 см Объемные Большие Декоративные Декорации на торжество слова на свадьбу
Доставка из г. Одесса
380 грн
Купить
НЕВАЛЯШКА — Деревянная Продукция
Работает
Цифра ОДИН ЕДИНИЦА С КОРОНОЙ НА ГОДИК 1 Из Пенопласта 115СМ Объемная Большая Декорации слова на день рождения
Доставка из г. Одесса
699 грн
Купить
НЕВАЛЯШКА — Деревянная Продукция
Работает
Цифра 1 ОДИН ЕДИНИЦА С КОРОНОЙ НА ГОДИК Из Пенопласта 60 см Объемная Большая Декорации слова на день рождения
Доставка из г. Одесса
499 грн
Купить
НЕВАЛЯШКА — Деревянная Продукция
Работает
Цифра 1 ОДИН ЕДИНИЦА С КОРОНОЙ НА ГОДИК Из Пенопласта 60 см Объемная Большая Декорации слова на день рождения
Доставка из г. Одесса
499 грн
Купить
НЕВАЛЯШКА — Деревянная Продукция
Работает
Световая объемная цифра 1 с подсветкой (с лампочками) Manific Decor для праздника из фанеры 100 * 55 * 15 см
Доставка по Украине
2 890 грн
Купить
Manific Decor
Работает
Универсальная легкая шпаклевка Mipa P12 Light 1 л (объемный вес 2 кг)
На складе
Доставка по Украине
273. 63 грн
63 грн
265.42 грн
Купить
AUTOMIX — все для авто и гостинично-ресторанного бизнеса
Работает
Часы 3d светящиеся в темноте объемные разборные с 4 цифрами точками и птичкой до 1м
На складе в г. Киев
Доставка по Украине
772 грн
Купить
Landis
Работает
Бездротові геймерські навушники Kotion Each G9000BT з підтримкою об’ємного звуку 7.1 Stereo Sound
Доставка по Украине
1 535 — 2 040 грн
от 2 продавцов
1 535 грн
Купить
Innovative.com.ua — Интернет-магазин
Работает
Игровая гарнитура EKSA E900 Pro с шумоподавлением и объемным звуком 7.1
На складе
Доставка по Украине
800 — 899 грн
от 2 продавцов
1 000 грн
800 грн
Купить
Techno.mix.te
Работает
Свеча Цифра 7 объемная Balloon золото — 1 шт
Доставка по Украине
26 грн
Купить
Интернет — магазин для кондитера
Работает
Часы 3d DIY настенные светящиеся в темноте большие и маленькие цифры + круги серебро до 1м
На складе в г. Киев
Киев
Доставка по Украине
772 грн
Купить
Landis
Как сделать объемную цифру своими руками: выбор материала, простые способы, порядок действий, описание с фото и рекомендации
- 6 Ноября, 2018
- Поделки
- София Ермакова
Объемные цифры, сделанные своими руками, часто можно увидеть на детских праздниках. Это легкое украшение, которое создаст праздничную атмосферу и послужит реквизитом для запоминающихся фото. Такие элементы декора вне конкуренции. Объемные цифры легкие, недорогие в исполнении, красивые. Они вызывают исключительно приятные эмоции. Оригинальная композиция требует творческого подхода, так что изготовление цифры займет не один час. В статье мы расскажем, как сделать объемную цифру.
Что понадобится для работы
Чаще всего можно увидеть объемные цифры, щедро украшенные цветочками, бахромой или помпонами из обычных столовых салфеток. Еще делают декор для детского дня рождения с помощью блесток и воздушных шаров. Тут все зависит от фантазии, тематики праздника и желания. Но внешние украшения скрывают каркас-основу, которая и позволяет цифре быть объемной. Основа обычно делается из картона, дерева или пенопласта. Чтобы сделать своими руками объемную цифру 2 (или любую другую), понадобятся такие материалы и инструменты:
Еще делают декор для детского дня рождения с помощью блесток и воздушных шаров. Тут все зависит от фантазии, тематики праздника и желания. Но внешние украшения скрывают каркас-основу, которая и позволяет цифре быть объемной. Основа обычно делается из картона, дерева или пенопласта. Чтобы сделать своими руками объемную цифру 2 (или любую другую), понадобятся такие материалы и инструменты:
- Картон. Чем его размеры больше, тем крупнее получится готовое украшение. Можно использовать коробки, в которых привозили бытовую технику, то есть те материалы, которые часто отправляются в мусорное ведро.
- Пенопласт. Можно купить пенопластовую панель в строительном магазине, склеить между собой несколько листов, чтобы цифра получилась толще.
- Однотонные бумажные салфетки (одной упаковки мало, лучше взять сразу несколько по 100-200 штук).
- Вместо салфеток подойдет гофрированная или любая другая тонкая бумага;
- ножницы, клей, нитки, простой карандаш и линейка, скотч, клей для пенопласта, дополнительные материалы для декора.
Как сделать для цифры из картона основу
Как сделать объемную цифру на день рождения? Весь процесс начинается с формирования основы: самой цифры 1, 2, 3 или любой другой. Можно делать объемными целые слова и фигуры (имя малыша, любимый персонаж для детского дня рождения, инициалы молодоженов, фигурку жениха и невесты для свадьбы и так далее). Особого внимания требует первый праздник малыша, поэтому многие мамы интересует тем, как сделать своими руками объемную цифру 1. Ребенок не запомнит оформление праздника, количество присутствующих и угощения, но можно сделать яркие и красочные фото, которые сохранят память о первом дне рождении.
Рассмотрим подробно, как сделать объемную цифру из картона. Если для основы вы выбрали именно этот материал, то нарисуйте на нем цифру необходимого размера и формы, вырежьте ее острым канцелярским ножом. Таких заготовок понадобится две. Можно обильно украсить объемным декором одну заготовку. Если предполагается создание именно объемной основы, то кроме второй заготовки потребуется вырезать полосы из картона. Их ширина зависит от того, насколько объемной вы хотите сделать цифру.
Их ширина зависит от того, насколько объемной вы хотите сделать цифру.
Чтобы полоска гнулась без заломов, через каждые 2-3 см сделайте насечки канцелярским ножом. С одной стороны прикрепите полоску по всему периметру цифры на скотч, затем наложите вторую часть заготовки и тоже хорошо закрепите. Можно клеить скотч по лицевой стороне, потому что все будет закрыто декором.
Заготовка для небольшого украшения
Из упаковок из-под продуктов получаются небольшие цифры. Если решите использовать коробку, в которой продавались кукурузные хлопья, сок или молоко, то перед началом процесса украшения цифры проклейте поверхность основы слоем папье-маше, чтобы не было видно заводского рисунка. Для оклейки возьмите густой клей ПВА и туалетную (газетную или однотонную тонкую) бумагу. Это придаст заготовке дополнительную прочность, потому что тонкий картон в процессе работы может разбухнуть и расплыться. Другой вариант — просто выбрать упаковку с фольгированной поверхностью. В таких выпускаются многие молочные продукты и соки.
Пенопластовая основа
Как сделать объемную цифру из салфеток и пенопласта? Если вы выбрали в качестве материала для основы пенопласт, то работать будет гораздо удобнее. Цифру вырежьте из бумаги или нарисуйте прямо на пенопласте, а затем вырежьте. Если лист материала слишком тонкий, склейте между собой несколько листов клеем для потолочной плитки. Удобнее всего работать с этим капризным материалом специальным инструментом.
Если есть возможность использовать профессиональный режущий инструмент с нагретой нихромовой нитью, обязательно этим воспользуйтесь. Подобный резак можно сделать из паяльника с закрепленной медной проволокой, но это только для создания объемных цифр в большом количестве. Хорошо режется пенопласт и обычным ножом по металлической линейке.
Какого размера делать объемную цифру
При создании декора для фотосессии или дня рождения маленького ребенка, лучше ориентироваться на рост именинника. На стол или для украшения дома номерки делают более компактные. При высоте цифры 65-70 см ее оптимальная ширина — 35 см, а глубина — 15 см. При высоте 82 см, ширина — 45 см, глубина — 12 см. Размер плоской фигурки — примерно 30 х 40 см. Это только приблизительные рекомендации. Можете сделать цифру другого размера.
При высоте цифры 65-70 см ее оптимальная ширина — 35 см, а глубина — 15 см. При высоте 82 см, ширина — 45 см, глубина — 12 см. Размер плоской фигурки — примерно 30 х 40 см. Это только приблизительные рекомендации. Можете сделать цифру другого размера.
Варианты украшений
Для декора используется любая тонкая бумага. Можно украсить цифру большими помпонами, объемными или плоскими цветами, бахромой и так далее. Для фигурки большого размера понадобится около 100-200 роз из бумаги. Это сообщаем вам для понимания масштабности работы. Желательно выбирать пышные цветы, например, розы или астры. Чтобы сэкономить время, боковые стороны можно обтянуть гофрированной бумагой. Можно украшать цифру одинаковыми или разными цветками, например, комбинировать два-три цвета и делать градиентные переходы. То же самое касается бахромы.
Как сделать розочки из бумаги
Как сделать объемную цифру своими руками? Пошагово весь процесс создания элемента декора с картонной основой выглядит следующим образом:
- На большом листе картона нарисовать заготовку — цифру необходимой формы и размера.

- Вырезать две заготовки-номерка и полосу из картона. Сделать канцелярским ножом насечки через каждые 2-3 см на полоске.
- Скрепить все элементы между собой с помощью скотча.
- Изготовить необходимое количество розочек из бумаги для декора. Это можно сделать разными способами, которые мы описываем ниже.
- Приклеить декор к заготовке в определенном порядке или хаотично, если используется несколько цветов. Для лицевой стороны лучше использовать нежные оттенки, а на края клеить более темные. Так фигура будет выглядеть еще объемнее. Для фиксации нельзя использовать шпажки, потому что композиция должна быть не только красивой и прочной, но и безопасной для ребенка.
Для изготовления самой простой розы понадобится нарисовать на квадрате цветной бумаги спираль и вырезать полоску по обозначенному контуру. Затем плотно сверните полоску, начиная от центра. Для прочности в основание конструкции можно добавить немного клея.
Чтобы сделать более естественные розы, нужна гофрированная бумага. Вырежьте 15 лепестков в форме сердец и 5 в форме капель. Каждый лепесток слегка растяните по направлению от центра к краям, чтобы придать более естественную форму. Подогните края с помощью ручки или карандаша. Теперь прикрепите к основе-проволоке лепестки-капельки, потом — лепестки-сердечки. При необходимости закрепить конструкцию клейкой лентой.
Вырежьте 15 лепестков в форме сердец и 5 в форме капель. Каждый лепесток слегка растяните по направлению от центра к краям, чтобы придать более естественную форму. Подогните края с помощью ручки или карандаша. Теперь прикрепите к основе-проволоке лепестки-капельки, потом — лепестки-сердечки. При необходимости закрепить конструкцию клейкой лентой.
Чтобы сделать розы, которые выглядят, как настоящие, нужно разрезать бумагу на полоски шириной 1-5 см. Из одного листа формата А4 получится до 20 розочек.
Как сделать объемные астры для декора
Для создания пышной астры нужно взять шесть салфеток и степлер. Салфетки сложите стопкой, вырежьте лепестки (закруглите края), скрепите в центре и разверните, немного сдвигая лепестки. Цветок распушите. Можно попробовать сделать края волнистыми. Интересно будет выглядеть цветок с зубчиками по краям. Для одного цветочка попробуйте использовать салфетки разных цветов, чтобы декор выглядел ярче и разнообразнее.
Объемная цифра в технике «торцевание»
Как сделать своими руками объемную цифру? Декор в технике «торцевание» позволит сделать очень пушистый элемент декора для детского праздника. Для украшения лучше взять гофрированную бумагу, но и из салфеток тоже получается неплохо. Бумагу разрежьте на квадраты, а затем вставьте в середину листа карандаш (не протыкая) и придавите его бумагой. Приложите бумагу с карандашом к поверхности, предварительно обмазанной клеем. Таким образом нужно заполнить всю поверхность объемной цифры. Когда все подсохнет, можно расправить декор руками и аккуратно обрезать все лишнее.
Для украшения лучше взять гофрированную бумагу, но и из салфеток тоже получается неплохо. Бумагу разрежьте на квадраты, а затем вставьте в середину листа карандаш (не протыкая) и придавите его бумагой. Приложите бумагу с карандашом к поверхности, предварительно обмазанной клеем. Таким образом нужно заполнить всю поверхность объемной цифры. Когда все подсохнет, можно расправить декор руками и аккуратно обрезать все лишнее.
Объемная цифра с бахромой
Это самый простой способ украшения объемной фигуры. Вам потребуется длинная полоса, поэтому удобнее будет использовать бумагу тишью. Как сделать объемную цифру своими руками? Бумагу сложите в аккуратный прямоугольник и надрежьте, а затем расправьте и распушите бахрому. К заготовке полосы можно прикреплять двусторонним скотчем. Так можно комбинировать цвета, чтобы получилась очень яркая цифра для декора детского мероприятия или фотосессии. Намного интереснее выглядит бахрома, которая наклеена волнами. В этом случае особенно хорошо, если цвета будут контрастными.
Цифра-фигурка для детского дня рождения
На основе простой цифры можно сделать тематический декор для праздника. Например, родители девочек устраивают детские вечеринки в стиле Минни Маус — это простой и эффективный вариант. Как своими руками сделать объемную цифру с тематическим уклоном? Обычную фигурку нужно просто украсить соответствующим образом. Например, обклейте большую цифру 3 (или другую) красными и черными салфетками в технике «торцевание», добавьте белые кружочки из бумаги, а из черного картона вырежьте два круга и закрепите их «на макушке» цифры (это будут ушки). Аналогично можно стилизовать цифру под любимого персонажа мультика. Достаточно использовать подходящий цвет и добавить несколько деталей из других материалов.
Зимний вариант цифры для декора
Как сделать объемную цифру необычной? Если вы решили украсить дом объемной поздравительной надписью или цифрой наступающего года, можно сделать декор украшения в соответствующем стиле. Если день рождения ребенка выпадает на зимнее время, также можно использовать новогоднюю тематику.
Кроме того, для зимнего варианта украшений отлично подходят помпоны из шерстяных ниток. Такая цифра будет смотреться мило и по-домашнему уютно. Основа делается из любого удобного материала: картона или пенопласта. Дерево не подходит, потому что такие цифры обычно просто красят.
Помпоны можно делать разных размеров из разноцветных ниток. Совсем маленькие помпоны можно изготавливать на вилке, а чуть побольше — просто на руках. Любые размеры доступны, если вы используете стандартный способ: наматывание шерстяных ниток на картонный круг-основу. На пальцах делать помпоны легче. Просто намотайте необходимое количество пряжи на пальцы, а затем перевяжите ниткой (оптимальная длина 20-25 см) между средним и безымянным. Снимите будущий помпон с руки и распушите. Для украшения объемной цифры таких заготовок понадобится очень много.
Дополнительно можно наклеить на фигурку декоративные снежинки, блестки, бусинки. При желании можно присыпать цифры и буквы «снегом», который делают из белого пенопласта. Для этого нужно отрезать от листа небольшие кусочки (или взять отходы, которые остались после изготовления цифры) и хорошенько их раскрошить. «Снег» насыпают на клеевую основу.
Для этого нужно отрезать от листа небольшие кусочки (или взять отходы, которые остались после изготовления цифры) и хорошенько их раскрошить. «Снег» насыпают на клеевую основу.
Похожие статьи
Поделки
Что можно сделать из желудей: поделки своими руками
Поделки
Поделки из каштанов своими руками
Поделки
Как сделать дом для Монстр Хай своими руками?
Поделки
Осенние поделки из природного материала: идеи, мастер-классы, полезные советы
Поделки
Обитатели Черного моря: поделки своими руками
Поделки
Оригинальные идеи поделок в садик
Цифры из салфеток своими руками
Многие согласятся, что очень важным моментом проведения любого праздника является его украшение.
Рукодельницы, которые любят мастерить элементы декора и украшений из подручных средств, могут взять на заметку декор из простых салфеток.
Из салфеток обычно делают цветы на ножках, конвертики для приборов на банкетный стол.
Содержимое обзора:
Украшение праздника
Праздничным трендом последних сезонов стали цифры из салфеток. Таким элементом можно выделить знаменательную дату в День рождения, или же сделать большую восьмерку в традиционный женский день.
Фото подобных украшений часто выкладывают молодые мамы, которые с любовью сделали цифру своими руками.
Украшение такого рода понравится как взрослому, так и ребенку. Еще до того, как мастерить цветочки, нужно определиться с цветом будущей композиции. Эффектно и празднично смотрятся цифры ярких расцветок.
Если планируется украшение праздника цветами или шарами, желательно подбирать цвет в тон другому декору.
Инвентарь для работы
Для того чтобы смастерить праздничный декор, необходимо сначала подготовить инвентарь для будущей работы.
Так как для изготовления цифры нам сперва понадобится сделать каркас, нужно запастись картонной бумагой. Лучше всего для этой цели подходит обычная упаковочная картонная коробка. Разрежем ее вдоль изгибов, чтобы материал был ровный, и его можно было согнуть в нужных местах.
Самые первые помощники в рукоделии – ножницы и нож. Инструменты должны быть обязательно острыми и наточенными. Это необходимо, чтобы контуры изделия были ровными, также хороший инструмент поможет не тратить много усилий на обрезку картона.
В изготовлении цветков нам также понадобится степлер и скрепки.
Чтобы линии для прорезывания были ровными, необходимо запастись линейкой. Линейка должна быть длиною до метра. Мерная лента тоже пригодится в работе.
Для того чтобы проклеить углы в нужных местах, в наличии нужно иметь клей и скотч. Скотч может быть как односторонним, так и двусторонним, в зависимости от того, каким вы привыкли работать.
Скотч может быть как односторонним, так и двусторонним, в зависимости от того, каким вы привыкли работать.
Ну и последним предметом для рукоделия являются сами салфетки. Чтобы цифры из салфеток были объемными, а сами салфетки хорошо складывались и держали форму, они должны быть двухслойными.
Предугадать необходимое количество запаса салфеток довольно трудно, все зависит от размера изделия, поэтому на всякий случай стоит купить на две упаковки больше.
Подготовка каркаса
После того, как точно прикинули и определились с размером будущего украшения, вырезаем два куска картона. На них нам нужно нарисовать две одинаковые по размеру цифры.
Чтобы нарисованные цифры были идентичными, можно чертить с помощью измерений на линейке. Или же есть другой вариант. Рисуем на одном куске картона цифры необходимых размеров, затем вырезаем ее ножницами и накладываем, как трафарет, на оставшийся кусок картона.
Теперь цифру можно обвести вокруг контура и так же вырезать ножницами. Итак, первые составляющие будущего украшения готовы.
Итак, первые составляющие будущего украшения готовы.
Далее нам необходимо сделать заготовки для боковой части нашего каркаса. Для того чтобы начертить боковые грани, нужно поставить две вырезанные цифры на пол рядом, в том виде, в котором в итоге будет выглядеть цифра.
Швейным сантиметром нужно измерить длину сгибаемого бокового каркаса со всех сторон. В зависимости от цифры, которую вы мастерите, может получиться разное количество необходимых дополнительных отрезков.
Например, если готовится цифра из салфеток на годик ребенку, в ней количество боковых граней будет меньше, чем, к примеру, в двойке. В среднем ширина такой цифры около 10-15 см, в зависимости от ее высоты.
После того как измерили необходимые части, опять наносим рисунок на картон и аккуратно вырезаем по контуру ножницами. Тут необходимо заметить, что на данном этапе можно использовать мягкий и уже согнутый картон, который служил каркасом внутри коробки. Это позволит легко согнуть боковые части и без труда закрепить их.
Поделки из пластилина для детей: мастер-класс + инструкция, как сделать своими руками. Фото, лучшие идеи, видео, секреты, отзывы
Осенние поделки: ТОП-200 фото лучших вариантов с эксклюзивным дизайном. Пошаговая инструкция, мастер-класс, секреты мастериц, отзывы + видео
Светильник-ночник своими руками — инструкция и советы по оформлению
С помощью широкого скотча закрепляем боковые части сначала на одной стороне цифры, а потом прикрепляем оставшуюся вторую часть первоначально вырезанного каркаса. Чтобы каркас легче склеить, широкий скотч нужно нарезать на длинные полоски.
Самый тяжелый этап работы пройден и каркас готов.
Цветы из салфеток
Теперь, когда картонный каркас ждет своего часа, начинаем готовить цветки. Тут придется потрудиться, потому что цветов должно быть очень много.
Сперва складываем нашу двухслойную салфетку в два раза. Получился маленький объемный квадратик. Теперь центр готовой салфетки прокалываем степлером и отрезаем у квадрата уголки, чтобы получился круг. Так выглядит заготовка для цветка.
Получился маленький объемный квадратик. Теперь центр готовой салфетки прокалываем степлером и отрезаем у квадрата уголки, чтобы получился круг. Так выглядит заготовка для цветка.
Можно сначала наделать таких заготовок из салфеток, а уже потом превращать их в цветы. У скрепленной салфетки поднимаем края, начиная с самого верхнего слоя. Последний нижний слой оставляем ровным.
Чтобы сделать объемную цифру с пышными цветками, сильно сжимаем края цветочков пальцами, а потом аккуратно расправляем «лепестки». Такая работа может занять несколько часов, но готовая декорация стоит потраченного времени.
Цветы могут быть разных расцветок. Белый цвет в композиции очень гармонично смотрится с любым оттенком.
Собираем цифры
Когда все части готовы, можно приступить к самому приятному этапу рукоделия – приклеиванию цветов. Для этого наносим каплю клея на нижний ровный слой цветка и аккуратно приклеиваем к каркасу.
Чтобы цветок хорошо держался, нужно хорошенько придавить его к картонной основе и несколько секунд подержать. Таким образом, необходимо обклеить все грани картонной заготовки цветами.
Таким образом, необходимо обклеить все грани картонной заготовки цветами.
Когда клей просохнет, аккуратно расправляем цветы из салфеток, и любуемся готовой работой.
Готовые цифры могут выглядеть совершенно уникально, если добавить в них немного особенного декора. Например, можно украсить каждый цветок блестящими камушками, или задекорировать готовую декорацию блестками.
Также можно сделать композицию из шаров, блестящих нитей и самой цифры. Такое украшение будет прекрасно смотреться в фотозоне праздника, порадует именинника и гостей.
Как видите, сделать цифру из салфеток своими руками совсем не сложно, главное знать, как подойти к процессу.
Фото цифр из салфеток своими руками
youtube.com/embed/R5WbP9NLpT8″ frameborder=»0″ allowfullscreen=»allowfullscreen»>Номер один логотип 3d объемная фигура 1 шаблон векторное изображение
Номер один логотип 3d объемная фигура 1 шаблон векторное изображение- лицензионные векторы
- 3d векторов
ЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Расшир. | |
|---|---|---|
| Печатный/редакционный | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменить | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по запросу |
Способы покупкиСравнить
Плата за изображение € 14,99 Кредиты € 1,00 Подписка € 0,69 Оплатить стандартные лицензии можно тремя способами. Цены евро евро .
Цены евро евро .
| Оплата с помощью | Цена изображения |
|---|---|
| Плата за изображение € 14,99 Одноразовый платеж | |
| Предоплаченные кредиты € 1 Загружайте изображения по запросу (1 кредит = 1 евро). Минимальная покупка 30р. | |
| План подписки От 0,69 € Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение € 39,99 Кредиты € 30,00Существует два способа оплаты расширенных лицензий. Цены евро евро .
| Оплата с помощью | Стоимость изображения |
|---|---|
Плата за изображение € 39,99 Оплата разовая, регистрация не требуется. | |
| Предоплаченные кредиты € 30 Загружайте изображения по запросу (1 кредит = 1 евро). | |
Дополнительные услугиПодробнее
Настроить изображение Доступно только с оплатой за изображение € 85,00Нравится изображение, но нужны лишь некоторые модификации? Пусть наши талантливые художники сделают всю работу за вас!
Мы свяжем вас с дизайнером, который сможет внести изменения и отправить вам изображение в выбранном вами формате.
Примеры
- Изменить текст
- Изменить цвета
- Изменение размера до новых размеров
- Включить логотип или символ
- Добавьте свою компанию или название компании
файлов включены
Загрузка сведений…
- Идентификатор изображения
- 5151058
- Цветовой режим
- RGB
- Художник
- попавкропа
Что такое объем? Значение, определение, формула, примеры, расчет
Что такое
Том ? Каждый трехмерный объект занимает некоторое пространство. Это пространство измеряется с точки зрения его объема. Объем определяется как пространство, занимаемое в границах объекта в трехмерном пространстве. Он также известен как мощность объекта.
Это пространство измеряется с точки зрения его объема. Объем определяется как пространство, занимаемое в границах объекта в трехмерном пространстве. Он также известен как мощность объекта.
Нахождение объема объекта может помочь нам определить объем, необходимый для заполнения этого объекта, например, количество воды, необходимое для заполнения бутылки, аквариума или резервуара для воды.
Объем трехмерных фигур:
Поскольку разные трехмерные объекты имеют разную форму, их объемы также различны. Давайте посмотрим на некоторые трехмерные фигуры и научимся вычислять их объем (V).
Сфера
Самый простой и распространенный тип трехмерной формы — это сфера. Некоторые примеры сфер, которые мы видим в повседневной жизни, включают шары, глобусы, декоративные светильники, апельсины и т. д. Самое простое измерение, которое можно сделать на сфере, — это ее радиус. Объем сферы вычисляется по ее радиусу.
Объем сферы = $\frac{4}{3}$ πr 3 , где r — радиус сферы.
Куб
Следующей простой и распространенной трехмерной формой является куб. Он определяется тем уникальным свойством, что каждая сторона куба имеет одинаковую длину. Некоторыми повседневными примерами предметов в форме куба являются игральные кости, кубики Рубика, кубики сахара, подарочные коробки и т. д. Объем куба рассчитывается по длине его стороны.
Объем куба = a 3 , , где a — длина каждой стороны куба.
Прямоугольная форма
Прямоугольная призма. В прямоугольном параллелепипеде длина сторон будет разной. Следующие обозначения используются для обозначения сторон прямоугольного параллелепипеда.
- Длина = l
- Ширина = b
- Высота = h
Все эти размеры используются для расчета объема прямоугольного параллелепипеда. Типичными примерами прямоугольных параллелепипедов являются книги, обувные коробки, кирпичи, матрацы и т. д.
д.
Объем кубоида = l x b x h
Цилиндр
Цилиндр также представляет собой трехмерную форму с круглым основанием и высотой разделение двух оснований. К повседневным предметам цилиндрической формы относятся бутылки с водой, ведра, свечи, банки и т. д. Объем цилиндра рассчитывается путем измерения радиуса основания и высоты.
Volume of a Cylinder = πr 2 h , where r is the radius of the base, and h is the height of the cylinder .
Конус
Конус — это трехмерная форма, которую мы обычно видим вокруг себя. Рожок для мороженого, праздничная шляпа, воронка или рождественская елка — все это примеры конуса. Конус представляет собой характерную трехмерную геометрическую фигуру, которая имеет плоскую поверхность и криволинейную поверхность, направленную вверх.
Объем конуса = $\frac{1}{3}$πr 2 h, , где r — радиус основания конуса, а h — высота конуса от основание к вершине.
Измерение объема
Объем вычисляется для трехмерных объектов и, следовательно, представляется в кубических единицах или другом формате записи кубических единиц; так как это обычно используется (единица измерения)³, например, кубические сантиметры, кубический дюйм, кубический фут, кубический метр и т. д. Если длина или радиус измеряются в сантиметрах, то объем измеряется в кубических сантиметрах (см 3 ). Если измерения в метрах, объем измеряется в кубических метрах (м 3 ).
Когда мы измеряем объем жидкостей (например, чтобы найти объем воды, который может вместить цилиндрическая бутылка), мы должны изменить значения в см 3 или м 3 на литры. Объем можно перевести из литров в сантиметры по следующей формуле.
1 л = 1000 см 3
1 l = 1000 ml
1000 cm 3 = 1000 ml
So, 1 см 3 = 1 мл
Заключение
Понимание математических понятий, таких как объем, становится интересным с помощью наглядных пособий, таких как интерактивные игры. Вы можете проверить игры, рабочие листы и решенные задачи по темам, подобным этой, на веб-сайте Splashlearn. Посетите https://www.splashlearn.com/, чтобы узнать новые концепции, развлекаясь.
Вы можете проверить игры, рабочие листы и решенные задачи по темам, подобным этой, на веб-сайте Splashlearn. Посетите https://www.splashlearn.com/, чтобы узнать новые концепции, развлекаясь.
Решенные примеры
1. У Генри есть цилиндрическая бутылка для воды с радиусом основания 5 см и высотой 10 см. Какой объем воды может храниться в бутылке?
Solution:
Volume of the bottle= πr 2 h
= π (5 x 5) x 10
= π x 250
= 3.14 x 250
= 785 см 3
= 785 мл (1 см 3 = 1 мл)
2. Риаз владеет мячом для крикета радиусом 3 см. Какой объем занимает мяч в сумке Риаза?
Решение:
Объем шара = $\frac{4}{3}$ πr 3
= $\frac{4}{3}$ x $\frac{22 {7}$ x (3 x 3 x 3)
= 113,14 см 3
3. Коническая елка изготовлена из глины. Высота дерева 14 дюймов, а диаметр основания 6 дюймов. Сколько глины используется? (используйте π = $\frac{22}{7}$)
Коническая елка изготовлена из глины. Высота дерева 14 дюймов, а диаметр основания 6 дюймов. Сколько глины используется? (используйте π = $\frac{22}{7}$)
Решение:
Диаметр = 6 дюймов
Радиус = $\frac{6}{2}$ = 3 дюйма
Объем глина = $\frac{1}{3}$ πr 2 h
= $\frac{1}{3}\times \frac{22}{7}\times 3\times 3\times 14
долларов = 132 кубических дюйма.
Практические задачи
l x l x l
b x b x b
h x h x h
l x b x h
Правильный ответ: l x b x h 9{3}$
Часто задаваемые вопросы
Является ли объем прямоугольной призмы таким же, как объем параллелепипеда?
Да, объем прямоугольной призмы такой же, как объем параллелепипеда. Кубоид имеет стороны неравной длины. Его объем рассчитывается по формуле l x b x h , где l, b и h — это различные измерения формы.
Как рассчитать объем неправильной формы?
Если вам нужно рассчитать объем фигуры, которая не является одной из правильных трехмерных фигур, разбейте неправильную форму на разные правильные формы. Добавьте отдельные объемы этих фигур, чтобы получить общий объем.
Добавьте отдельные объемы этих фигур, чтобы получить общий объем.
Как проще всего определить громкость?
Объем – это пространство, занимаемое любым объектом. Это занимаемое пространство зависит от формы объекта. Лучший способ понять — исследовать различные предметы и найти объем, занимаемый ими.
Что следует учитывать при расчете объемов различной формы?
Важной проверкой перед расчетом объема любой формы должно быть то, что все измерения должны быть в одних и тех же единицах измерения. Если одно измерение указано в см, а другое в м, перед расчетом объема конвертируйте оба значения в см или м.
Рисунки и данные в разделе Электрическое поле вызывает объемные изменения в головном мозге человека
Электрическое поле (EF) и изменение объема в 85 областях мозга.
Первый ряд верхней панели: средняя EF по 85 областям мозга; второй ряд: размер эффекта изменения объема между исходным уровнем и в конце курса ЭСТ в 85 регионах. Нижняя панель слева: величина эффекта правосторонних односторонних стимуляций была постоянно выше на правой стороне, чем на левой. Нижняя панель справа: график рассеяния региональной EF по сравнению с региональным изменением объема (r = 0,38; p <0,001; df = 83; t = 3,77). (d) = размер эффекта d Коэна..
Нижняя панель слева: величина эффекта правосторонних односторонних стимуляций была постоянно выше на правой стороне, чем на левой. Нижняя панель справа: график рассеяния региональной EF по сравнению с региональным изменением объема (r = 0,38; p <0,001; df = 83; t = 3,77). (d) = размер эффекта d Коэна..
Различия латеральности в EF и ∆vol (верхняя панель), а также взаимосвязь между латеральностью между EF/∆vol (нижняя панель).
Линия регрессии указывает на корреляцию между индексами латеральности EF и изменением объема (r = 0,32; p<0,05; df = 40; t = 2,13).
Индивидуальная специфическая связь между ФВ и изменением объема гиппокампа.
Слева: диаграмма рассеяния EF в зависимости от изменения объема в гиппокампе (t = 5,97, df = 300, r = 0,33, p <0,0001, левая и правая стороны вместе). Слева имеется значительная взаимосвязь (оранжевые точки; t = 4,53, df = 149, r = 0,35, p < 0,0001), а справа нет (вероятно, из-за эффекта потолка) (t = 1,59, df = 149, г = 0,13, р = 0,11). Справа: разница в изменении объема правого и левого гиппокампа значительна (t = 7,76, df = 150, средняя разница = 0,011, p <0,0001).
Слева имеется значительная взаимосвязь (оранжевые точки; t = 4,53, df = 149, r = 0,35, p < 0,0001), а справа нет (вероятно, из-за эффекта потолка) (t = 1,59, df = 149, г = 0,13, р = 0,11). Справа: разница в изменении объема правого и левого гиппокампа значительна (t = 7,76, df = 150, средняя разница = 0,011, p <0,0001).
ФВ гиппокампа и изменение объема.
Чтобы проверить специфичность наших измерений в левом гиппокампе (результаты с поправкой на FDR), мы переставили метки в 85 ROI, как для изменений объема (слева), так и для значений EF (справа), и рассчитали корреляции между EF и объемом. изменение этих регионов соответственно. Таким образом мы получили 85 различных значений, одно из которых было «правильной» корреляцией, обозначенной красными точками. «Правильные» корреляции между EF и соответствующим объемом превзошли другие корреляции (находившиеся в пяти верхних процентилях) из несовпадающих пар, указывая на то, что наши результаты не были просто общей корреляцией с некоторыми средними значениями по регионам, что еще больше усиливало случайную связь. связь между КВ и изменением объема.
связь между КВ и изменением объема.
Индивидуальная специфическая связь между ФВ и изменением объема в миндалевидном теле.
Слева: диаграмма рассеяния EF в зависимости от изменения объема в миндалевидном теле (t = 11,35, df = 300, r = 0,55, p<0,0001; левая и правая стороны вместе). Как левое (оранжевые точки), так и правое (синие точки) полушария демонстрируют очень значимые взаимосвязи (t = 4,01, df = 149, г = 0,31, р = 0,0001; и t = 4,02, df = 149, r = 0,31, p = 0,0001). Справа: разница в изменении объема правой и левой миндалины значительна (t = 13,58, df = 150, средняя разница = 0,029, p<0,0001).
ФВ миндалевидного тела и изменение объема.
Чтобы проверить специфичность наших измерений в левой миндалине (результаты с поправкой на FDR), мы переставили метки в 85 ROI, как для изменений объема (слева), так и для значений EF (справа), и рассчитали корреляции между EF и объемом. изменение этих регионов соответственно. Таким образом мы получили 85 различных значений, одно из которых было «правильной» корреляцией, обозначенной красными точками. «Правильные» корреляции между EF и соответствующим объемом превзошли другие корреляции (находившиеся в пяти верхних процентилях) из несовпадающих пар, указывая на то, что наши результаты не были просто общей корреляцией с некоторыми средними значениями по регионам, что еще больше усиливало случайную связь. связь между КВ и изменением объема.
изменение этих регионов соответственно. Таким образом мы получили 85 различных значений, одно из которых было «правильной» корреляцией, обозначенной красными точками. «Правильные» корреляции между EF и соответствующим объемом превзошли другие корреляции (находившиеся в пяти верхних процентилях) из несовпадающих пар, указывая на то, что наши результаты не были просто общей корреляцией с некоторыми средними значениями по регионам, что еще больше усиливало случайную связь. связь между КВ и изменением объема.
Иллюстрация методов.
Мы проанализировали данные продольной структурной МРТ 151 человека. Мы рассчитали изменение объема и величину электрического поля в 85 областях коры головного мозга и подкорковых структур человека.
Таблицы
Взаимосвязь между изменениями объема и EF у разных людей (Δ Vol ~ EF + Age + ECTnum).

| roi | t EF | p EF | t Age | t ECTnum | BH EF FDR | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Δ VOL Левый. Мозжечок. Кора | −0.3668 | 0.7143 | −0.1150 | 1.9368 | 0.8205 | |||||||||||||||
| 2 | Δ VOL Left.Thalamus.Proper | 0.0244 | 0.9805 | −0.4046 | 2.8696 | 0.9952 | |||||||||||||||
| 3 | Δ VOL Left. Caudate Caudate | 0.6555 | 0.5132 | −0.8301 | 2.6428 | 0.6924 | |||||||||||||||
| 4 | Δ VOL Left.Putamen | 0.5737 | 0.5671 | −0.5992 | 1.3203 | 0.7212 | |||||||||||||||
| 5 | Δ VOL Left.Pallidum | 0.0060 | 0.9952 | 0.1026 | 1.2295 | 0.9952 | |||||||||||||||
| 6 | Δ VOL Brain.Stem | 1.2114 | 0.2278 | 0.8536 | 1.2309 | 0.4466 | |||||||||||||||
| 7 | Δ VOL Left. Hippocampus Hippocampus | 4.5102 | 0.0000 | −2.6814 | 3.3221 | 0.0012 | |||||||||||||||
| 8 | Δ VOL Left.Amygdala | 3.9069 | 0.0001 | − 1.0572 | 2.1018 | 0.0061 | |||||||||||||||
| 9 | Δ VOL Left.Accumbens.area | 2.0238 | 0.0449 | −3.4456 | 1.7246 | 0.1737 | |||||||||||||||
| 10 | Δ VOL Left.VentralDC | 0.1740 | 0.8621 | 0.0605 | 2.2614 | 0.9395 | |||||||||||||||
| 11 | Δ VOL Right. Cerebellum.Cortex Cerebellum.Cortex | − 0,5564 | 0,5788 | 0,0677 | 1,3212 | 0,7235 | |||||||||||||||
| 12 | Δ vol Права.0025| 0.3541 | 4.0787 | 0.7712 | | |||||||||||||||||
| 13 | Δ VOL Right.Caudate | 1.2293 | 0.2210 | 1.0254 | 1.5097 | 0.4466 | |||||||||||||||
| 14 | Δ VOL Right. Putamen | 1.0724 | 0.2854 | −0.5112 | 1.4987 | 0.4756 | |||||||||||||||
| 15 | Δ VOL Right.Pallidum | 0. 6045 6045 | 0.5465 | 0.8016 | 2.9589 | 0.7181 | |||||||||||||||
| 16 | Δ VOL Right.Hippocampus | 1.5090 | 0.1336 | −1.2924 | 3.2473 | 0.3441 | |||||||||||||||
| 17 | Δ VOL Right.Amygdala | 2.9945 | 0.0032 | −0.6087 | 4.2603 | 0.0344 | |||||||||||||||
| 18 | Δ VOL Right.Accumbens.area | 1.9563 | 0.0524 | −0.8782 | 3.5228 | 0.1937 | |||||||||||||||
| 19 | Δ VOL Right. VentralDC VentralDC | 0.3488 | 0.7278 | 0.5197 | 0.7438 | 0.8248 | |||||||||||||||
| 20 | Δ VOL ctx.lh.bankssts | 1.1757 | 0.2417 | −0.4102 | 2.5801 | 0.4466 | |||||||||||||||
| 21 | Δ VOL ctx.lh.caudalanteriorcingulate | 1.3404 | 0.1823 | −1.2881 | 2.2330 | 0.4254 | |||||||||||||||
| 22 | Δ VOL ctx.lh.caudalmiddlefrontal | −1.8989 | 0.0596 | −0.3804 | 2.0087 | 0.2112 | |||||||||||||||
| 23 | Δ VOL ctx. lh.cuneus lh.cuneus | 0.9827 | 0.3274 | 0.1037 | 2.0348 | 0.5352 | |||||||||||||||
| 24 | Δ VOL ctx.lh.entorhinal | 3.2229 | 0.0016 | −1.2447 | 1.6659 | 0.0335 | |||||||||||||||
| 25 | Δ VOL ctx.lh.fusiform | 3.0717 | 0.0026 | −0.1806 | 2.1319 | 0.0344 | |||||||||||||||
| 26 | Δ VOL ctx.lh.inferiorparietal | 1.5131 | 0.1325 | 0.8515 | 2.3077 | 0.3441 | |||||||||||||||
| 27 | Δ VOL ctx. lh.inferiortemporal lh.inferiortemporal | 2.6985 | 0.0078 | 0.6415 | 1.9131 | 0.0577 | |||||||||||||||
| 28 | Δ VOL CTX.LH.ISTHMUSCULELATE | -0,3275 | 0,7438 | -0,4344 | 2,9060 | 0,8319 | 0,8319 | 140,8319 | |||||||||||||
| 0,8319 | 96666660,8319.0622 | 1.1916 | 0.2354 | 0.3669 | 1.2752 | 0.4466 | |||||||||||||||
| 30 | Δ VOL ctx.lh.lateralorbitofrontal | 1.4274 | 0. 1557 1557 | −0.0081 | 1.5758 | 0.3780 | |||||||||||||||
| 31 | Δ VOL ctx.lh.lingual | 0.1391 | 0.8896 | 0.3506 | 2.4745 | 0.9572 | |||||||||||||||
| 32 | Δ VOL ctx.lh.medialorbitofrontal | 1.0744 | 0.2845 | −0.1246 | 1.1852 | 0.4756 | |||||||||||||||
| 33 | Δ VOL ctx.lh.middletemporal | 2.0679 | 0.0405 | −0.3780 | 2.2600 | 0.1720 | |||||||||||||||
| 34 | Δ VOL ctx.lh.parahippocampal | 1. 2683 2683 | 0.2068 | −0.2446 | 2.8373 | 0.4466 | |||||||||||||||
| 35 | Δ VOL ctx.lh.paracentral | −2.0829 | 0.0391 | 0.2511 | 4.0937 | 0.1720 | |||||||||||||||
| 36 | Δ VOL ctx.lh.parsopercularis | −0.6949 | 0.4883 | −0.7822 | 1.8435 | 0.6694 | |||||||||||||||
| 37 | Δ VOL ctx.lh.parsorbitalis | 0.8057 | 0.4218 | −1.0427 | 0.9524 | 0.6289 | |||||||||||||||
| 38 | Δ VOL ctx. lh.parstriangularis lh.parstriangularis | 0.8228 | 0.4120 | −1.2157 | 2.7977 | 0.6254 | |||||||||||||||
| 39 | Δ Vol CTX.LH.PericalCarine | 0,4426 | 0,6587 | −0,0479 | 1,8463 | 0,7712 | |||||||||||||||
| 0,7712 | |||||||||||||||||||||
| 0.8692 | 0.3862 | −1.7655 | 2.5145 | 0.5969 | |||||||||||||||||
| 41 | Δ VOL ctx.lh.posteriorcingulate | −0.8698 | 0.3859 | −0.6961 | 3.3193 | 0.5969 | |||||||||||||||
| 42 | Δ VOL ctx. lh.precentral lh.precentral | −0.7279 | 0.4679 | −1.2884 | 2.4234 | 0.6682 | |||||||||||||||
| 43 | Δ VOL ctx.lh.precuneus | −1.5879 | 0.1145 | −0.4353 | 3.6729 | 0.3441 | |||||||||||||||
| 44 | Δ VOL ctx.lh.rostralanteriorcingulate | 1.3315 | 0.1852 | −0.4449 | 0.5630 | 0.4254 | |||||||||||||||
| 45 | Δ VOL ctx.lh.rostralmiddlefrontal | −0.7192 | 0.4732 | −1.6205 | 1.1936 | 0.6682 | |||||||||||||||
| 46 | Δ VOL ctx. lh.superiorfrontal lh.superiorfrontal | −1.2073 | 0.2293 | −0.5851 | 2.1065 | 0.4466 | |||||||||||||||
| 47 | Δ VOL ctx .lh.superiorParietal | −1,7423 | 0,0836 | 0,6952 | 3,3288 | 0,2734 | |||||||||||||||
| 0.0240 | −2.0868 | 1.6393 | 0.1199 | ||||||||||||||||||
| 49 | Δ VOL ctx.lh.supramarginal | 0.5717 | 0.5685 | −0.2467 | 2. 1282 1282 | 0.7212 | |||||||||||||||
| 50 | Δ VOL ctx.lh.frontalpole | −0.2029 | 0.8395 | −0.2904 | 0.4776 | 0.9267 | |||||||||||||||
| 51 | Δ VOL ctx.lh.temporalpole | 2.5288 | 0.0125 | −0.0731 | 1.3167 | 0.0762 | |||||||||||||||
| 52 | Δ VOL ctx.lh.transversetemporal | 0.4387 | 0.6616 | −0.4617 | 2.1817 | 0.7712 | |||||||||||||||
| 53 | Δ VOL ctx.rh.bankssts | 0.1121 | 0. 9109 9109 | 2.0777 | 2.9991 | 0.9678 | |||||||||||||||
| 54 | Δ VOL ctx.rh.caudalanteriorcingulate | −1.4295 | 0.1551 | 1.2935 | 2.4016 | 0.3780 | |||||||||||||||
| 55 | Δ VOL ctx.rh.caudalmiddlefrontal | -2,9569 | 0,0036 | 1,6943 | 2,6065 | 0,0344 | |||||||||||||||
| 56 | Δ Vol CTX.RHUNE | Δ Vol CTX.RHUNE | Δ Vol CTX.RHUNE | .0025 | −1.1806 | 2.4017 | 0.9952 | ||||||||||||||
| 57 | Δ VOL ctx. rh.entorhinal rh.entorhinal | 1.2514 | 0.2129 | 0.7897 | 2.4722 | 0.4466 | |||||||||||||||
| 58 | Δ VOL CTX.RH.FUSIFORM | 1,5380 | 0,1263 | 0,797 | 4,7854 | 0,3441 | |||||||||||||||
| 0,3441 | |||||||||||||||||||||
| 0,3441 | .0025 | −2.9902 | 0.0033 | 1.6520 | 0.7114 | 0.0344 | |||||||||||||||
| 60 | Δ VOL ctx.rh.inferiortemporal | 0.9300 | 0. 3540 3540 | 1.9310 | 3.3455 | 0.5677 | |||||||||||||||
| 61 | Δ VOL ctx.rh.isthmuscingulate | 0.0325 | 0.9741 | 0.4230 | 1.1493 | 0.9952 | |||||||||||||||
| 62 | Δ VOL ctx.rh.lateraloccipital | 1.1796 | 0.2401 | 0.6095 | 1.5161 | 0.4466 | |||||||||||||||
| 63 | Δ VOL ctx.rh.lateralorbitofrontal | 0.5347 | 0.5937 | 0,3393 | 2,9240 | 0,7314 | |||||||||||||||
| 64 | Δ VOL CTX.RH.LIGLEAL | —0,0753 | —0,0753 | —0,0753 | —0,0753 | —0,0753 | .0.9865 | ||||||||||||||
| 65 | Δ VOL ctx.rh.medialorbitofrontal | 0.7090 | 0.4795 | 1.5479 | 2.3419 | 0.6682 | |||||||||||||||
| 66 | Δ VOL ctx.rh.middletemporal | -0,6005 | 0,5492 | 2,1275 | 3,6781 | 0,7181 | |||||||||||||||
| 67 | Δ | 0.5057 | 3.1874 | 0.3441 | |||||||||||||||||
| 68 | Δ VOL ctx.rh.paracentral | −3.5101 | 0.0006 | 2.1809 | 2.2718 | 0. 0170 0170 | |||||||||||||||
| 69 | Δ Vol CTX.RH.Parsopercularis | −2.5585 | 0,0116 | 2,8854 | 2,9459 | 0,0756 | 0,0756 | 2,94590,0756 | 2,94590,0756 | 2,9459.0622 | 1.0872 | 0.2788 | −0.5812 | 2.3737 | 0.4756 | ||||||
| 71 | Δ VOL ctx.rh.parstriangularis | −1.2468 | 0.2146 | 1.0686 | 2.6086 | 0.4466 | |||||||||||||||
| 72 | Δ VOL ctx.rh.pericalcarine | 1. 5878 5878 | 0.1146 | −0.0096 | 2.2815 | 0.3441 | |||||||||||||||
| 73 | Δ VOL ctx.rh.postcentral | −1.7565 | 0.0812 | 1.2943 | 3.0605 | 0.2734 | |||||||||||||||
| 74 | Δ VOL ctx.rh.posteriorcingulate | −1.5171 | 0.1315 | 2.0716 | 1.4731 | 0.3441 | |||||||||||||||
| 75 | Δ VOL ctx.rh.precentral | −2.4918 | 0.0139 | 0.9967 | 3.7013 | 0.0762 | |||||||||||||||
| 76 | Δ VOL ctx. rh.precuneus rh.precuneus | −2.0231 | 0.0450 | −0.1921 | 2.5419 | 0.1737 | |||||||||||||||
| 77 | Δ VOL ctx.rh. rostralanteriorcingulate | 2.2083 | 0.0288 | 1.3734 | 2.3606 | 0.1362 | |||||||||||||||
| 78 | Δ VOL ctx.rh.rostralmiddlefrontal | −2.6842 | 0.0081 | 0.5804 | 2.2235 | 0.0577 | |||||||||||||||
| 79 | Δ VOL ctx.rh.superiorfrontal | −3.0013 | 0.0032 | 1.1011 | 3.2699 | 0. 0344 0344 | |||||||||||||||
| 80 | Δ Vol CTX.RH.SuperiorParietal | -2,7495 | 0,0067 | 0,9014 | 2,0779 | 0, | 2,0779 | 0, | 2,0779 | 0, | 2,0779 | 0, | 2,0779 | 0,9014 | 2,0779 | 0,9014 | .0621 ctx.rh.superiortemporal0.4377 | 0.6623 | 1.2455 | 4.4002 | 0.7712 |
| 82 | Δ VOL ctx.rh.supramarginal | −2.4794 | 0.0143 | 2.7408 | 3. 0429 0429 | 0.0762 | |||||||||||||||
| 83 | Δ VOL ctx.rh.frontalpole | 1.1256 | 0.2623 | −0.1784 | 1.9185 | 0.4644 | |||||||||||||||
| 84 | Δ VOL ctx.rh.temporalpole | 0.7274 | 0.4682 | 0.5099 | 3.7696 | 0.6682 | |||||||||||||||
| 85 | Δ VOL ctx.rh.transversetemporal | 1.1426 | 0,2551 | 0,6448 | 3,2405 | 0,4614 |
Клиническая и демографическая сводка.
| Таблица 2A Общая сумма | |||||||
|---|---|---|---|---|---|---|---|
| САЙТ | N | Возраст (SD) | . (MED. Free, SSRI/SNRI, TCA), AP, SSRI/SNRI, SNRI/SNRI, SSRI/SNRI, SSRI/SNRI, SSRI/SNRI, TCA). ECT | Baseline MADRS | Δ MADRS (%) | ||
| All | 151 | 57.5 (17.1) | 69,65,10,62 | 10.6 | 33.9 | 61.3 | |
| Female | 92 | 56.4 (18.4) | 42,36,8,42 | 10.4 | 34.4 | 63.4 | |
| Male | 59 | 59.3 (14.7) | 27 ,29,2,20 | 10.9 | 33.3 | 58.1 | |
| Table 2B Site Summary | |||||||
| Site | N | Age (mean) | Age (sd) | Baseline MADRS | Δ MADRS (%) | ||
| 1 | 30 | 39. 87 87 | 12.68 | 40.73 | 45.12 | ||
| 2 | 33 | 64.48 | 8.93 | 31.36 | 69.48 | ||
| 3 | 16 | 73.62 | 12.45 | 29.56 | 77.24 | ||
| 4 | 23 | 46.87 | 9.19 | 29.96 | 43.18 | ||
| 5 | 2 | 62.50 | 0.71 | 36. 75 75 | 32.03 | ||
| 6 | 18 | 48.50 | 16.77 | 33.83 | 57.12 | ||
| 7 | 29 | 72.66 | 7.57 | 35.07 | 79.13 | ||
* мед. бесплатно: без лекарств, СИОЗС: селективный ингибитор обратного захвата серотонина, СИОЗСН: ингибиторы обратного захвата серотонина и норадреналина, ТЦА: трициклические антидепрессанты, АП: антипсихотические препараты, пациентов, получавших ингибиторы МАО, не было.
Дополнительные файлы
Исходный код 1
После того, как EF и ΔVol были собраны в 85 ROI у 151 субъекта, все остальные расчеты проводились в среде R.

Этот файл представляет собой исходный код этих расчетов, организованный в организационном режиме (https://orgmode.org/) для воспроизводимости.
- https://cdn.elifesciences.org/articles/49115/elife-49115-code1-v2.org
Скачать elife-49115-code1-v2.org
Дополнительный файл 1
Изменения объема после электросудорожной терапии (ЭСТ).
Один образец t-критерия в каждой области интереса. В таблице указаны t, нескорректированное значение p, размер эффекта Коэна d и значения p с поправкой на FDR. Эта выборка представляет собой подгруппу недавней публикации из 331 субъекта (Ousdal et al., 2019). В отличие от этой публикации, мы включили пациентов с RUL только с размещением электродов.
- https://cdn.elifesciences.org/articles/49115/elife-49115-supp1-v2.
 docx
docxСкачать elife-49115-supp1-v2.docx
Дополнительный файл 2
Латеральность изменения объема после RUL ECT.
В таблице представлены результаты 42 парных t-тестов между изменениями объема правой и левой части соответствующих областей. В таблице указаны t, нескорректированное значение p, среднее значение, величина эффекта d Коэна и значения p с поправкой на FDR.
- https://cdn.elifesciences.org/articles/49115/elife-49115-supp2-v2.docx
Скачать elife-49115-supp2-v2.docx
Дополнительный файл 3
Взаимосвязь между клиническим ответом и изменением объема у разных людей.
В таблице указаны значения t соответствующих клинических переменных, смоделированных как фиксированные эффекты: изменение объема, возраст и количество ЭСТ.

- https://cdn.elifesciences.org/articles/49115/elife-49115-supp3-v2.docx
Скачать elife-49115-supp3-v2.docx
Дополнительный файл 4
Взаимосвязь между клинической реакцией и электрическим полем у разных людей.
В таблице указаны значения t соответствующих клинических переменных, смоделированных как фиксированные эффекты: электрическое поле, возраст и количество ЭСТ.
- https://cdn.elifesciences.org/articles/49115/elife-49115-supp4-v2.docx
Скачать elife-49115-supp4-v2.docx
Дополнительный файл 5
Взаимосвязь между исходным объемом и возрастом по 85 ROI.
- https://cdn.elifesciences.
 org/articles/49115/elife-49115-supp5-v2.docx
org/articles/49115/elife-49115-supp5-v2.docxСкачать elife-49115-supp5-v2.docx
Дополнительный файл 6
Сводка МРТ.
В таблице указаны параметры получения структурных изображений по сайтам.
- https://cdn.elifesciences.org/articles/49115/elife-49115-supp6-v2.docx
Скачать elife-49115-supp6-v2.docx
Прозрачная форма отчетности
- https://cdn.elifesciences.org/articles/49115/elife-49115-transrepform-v2.pdf
Скачать elife-49115-transrepform-v2.pdf
Ссылки для скачивания
Список ссылок, состоящий из двух частей, для загрузки статьи или частей статьи в различных форматах.
Открытые цитаты (ссылки для открытия цитат из этой статьи в различных онлайн-сервисах управления ссылками)
- Менделей
- ЧитатьКуб»>
Процитируйте эту статью (ссылки для загрузки цитат из этой статьи в форматах, совместимых с различными инструментами управления ссылками)
- Миклош Аргелан
- Лейф Олтедаль
- Чжи-Де Дэн
- Бенджамин Уэйд
- Маром Биксон
- Андреа Джоанланн
- Сохаг Сангани
- Хауке Барч
- Марта Кано
- Андерс М Дейл
- Удо Даннловски
- Аннемик Долс
- Верена Эннекинг
- Рэндалл Эспиноза
- Уте Кесслер
- Кэтрин Л Нарр
- Кетил Дж Эдегор
- Мардиен Л Удега
- Ронни Редлих
- Макс Л Стек
- Акихиро Такамия
- Луиза Эмселл
- Филип Букарт
- Паскаль Синарт
- Хесус Пухоль
- Индира Тендолкар
- Филип ван Эйндховен
- Георгиос Петридес
- Анил К Малхотра
- Кристофер Эбботт
(2019)
Электрическое поле вызывает объемные изменения в мозгу человека
eLife 8 :e49115.
https://doi.org/10.7554/eLife.49115
- Скачать БибТекс
- Скачать .RIS
| Определение | Формулы
Создано Ханной Памула, кандидатом наук, Петром Малеком и Матеушем Мухой
Рецензировано Богной Шик и Джеком Боуотером
Последнее обновление: 20 июня 2022 г.
Содержание:- Что такое объем? — Определение объема
- Единицы объема и таблица преобразования
- Как рассчитать объем? — Формулы объема
- Калькулятор объема и инструменты, предназначенные для конкретных форм
- Как пользоваться калькулятором объема?
- Измерение объема твердых тел, жидкостей и газов
- Как найти объем прямоугольника по сравнению с объемом коробки
- Применение в реальной жизни
- Часто задаваемые вопросы наиболее распространенные трехмерные тела.
 Прежде чем мы перейдем к тому, как рассчитать объем, вы должны знать определение объема. Объем отличается от площади, которая представляет собой объем пространства, занимаемый двумерной фигурой. Таким образом, вы можете запутаться, как найти объем прямоугольника и как найти объем коробки. Калькулятор поможет вычислить объем сферы, цилиндра, куба, конуса и прямоугольных тел.
Прежде чем мы перейдем к тому, как рассчитать объем, вы должны знать определение объема. Объем отличается от площади, которая представляет собой объем пространства, занимаемый двумерной фигурой. Таким образом, вы можете запутаться, как найти объем прямоугольника и как найти объем коробки. Калькулятор поможет вычислить объем сферы, цилиндра, куба, конуса и прямоугольных тел.Что такое объем? — Определение объема
Объем — это объем пространства, которое занимает объект или вещество. Обычно под объемом контейнера понимается его вместимость, а не объем пространства, который вытесняет сам контейнер. Кубический метр (м 3 ) — единица измерения объема в системе СИ.
Однако термин громкость может также относиться ко многим другим вещам, таким как
- степень громкости или интенсивность звука (вы можете проверить наш калькулятор шумового загрязнения или калькулятор дБ)
- количество или количество чего-либо (обычно большое количество)
- формальное слово для книги или одной из связанных книг.

Единицы объема и таблица преобразования
Популярные единицы объема:
- Метрические единицы объема
- Кубические сантиметры (см³)
- Кубические метры (м³)
- Литры (л, л)
- Миллилитры (мл, мл)
- Стандарт США, Великобритания
- Унция жидкости (жидкая унция)
- Кубический дюйм (куб. дюйм)
- Кубический фут (куб. фут)
- Чашки
- Пинты (pt)
- Кварты (кварты)
- Галлоны (гал)
Если вам нужно преобразовать единицы объема, вы можете использовать наш отличный конвертер объема. Еще один полезный инструмент — калькулятор граммов в чашках, который может помочь, если вы хотите использовать рецепт еды из другой страны. Обратите внимание, что это не простое преобразование, а переход от веса (граммы) к единице объема (стаканам) — поэтому вам нужно знать тип ингредиента (точнее, его плотность).

Кроме того, вы можете взглянуть на эту аккуратную таблицу преобразования единиц измерения объема, чтобы узнать коэффициент преобразования в мгновение ока:
кубических дюйма кубических фута кубических ярда американские галлоны жидкости американские сухие галлоны имп галлонов жидкости баррелей (нефть) чашки унции жидкости (Великобритания) жидких унций (США) пинты (Великобритания) кубический метр 6,1 10 4 35,3 1,30 8 264,2 227 220 6,29 4227 3,52 10 4 3,38 10 4 1760 кубический дециметр 61.  02
020,035 1,3 10 -3 0,264 0,227 0,22 0,006 4,23 35,2 33,8 1,76 кубический сантиметр 0,061 3,5 10 -5 1,3 10 -6 2,64 10 -4 2,27 10 -4 2,2 10 -4 6,29 10 -6 4,2 10 -3 3,5 10 -2 3,34 10 -2 1,76 10 3 кубический миллиметр 6,1 10 -5 3,5 10 -8 1,31 10 -9 2,64 10 -7 2,27 10 -7 2,2 10 -7 6,3 10 -9 4,2 10 -6 3,5 10 -5 3,4 10 -5 1,76 10 -6 гектолитры 6,1 10 3 3,53 0,13 26,4 22,7 22 0,63 423 3,5 10 3 3381 176 литра 61 3,5 10 -2 1,3 10 -3 0,26 0,23 0,22 6,3 10 -3 4,2 35,2 33,8 1,76 сантилитров 0,61 3,5 10 -4 1,3 10 -5 2,6 10 -3 2,3 10 -3 2,2 10 -3 6,3 10 -5 4,2 10 -2 0,35 0,338 1,76 10 -2 мл 6,1 10 -2 3,5 10 -5 1,3 10 -6 2,6 10 -4 2,3 10 -4 2,2 10 -4 6,3 10 -6 4,2 10 -3 3,5 10 -2 3,4 10 -2 1,76 10 -3 кубических дюйма 1 5,79 10 -4 2,1 10 -5 4,3 10 -3 3,7 10 -3 3,6 10 -3 10 -4 6,9 10 -2 0,58 0,55 2,9 10 -2 кубических фута 1728 1 0,037 7,48 6,43 6,23 0,18 119,7 997 958 49,8 кубических ярда 4,7 10 4 27 1 202 173,6 168,2 4,8 3232 2,69 10 4 2,59 10 4 1345 американские жидкие галлоны 231 0,134 4,95 10 -3 1 0,86 0,83 0,024 16 133,2 128 6,7 галлоны США, сухие 268,8 0,156 5,76 10 -3 1,16 1 0,97 0,028 18,62 155 148,9 7,75 имп галлонов жидкости 277,4 0,16 5,9 10 -3 1,2 1,03 1 0,029 19,2 160 153,7 8 баррели (нефть) 9702 5,61 0,21 42 36,1 35 1 672 5596 5376 279,8 чашки 14,4 8,4 10 -3 3,1 10 -4 6,2 10 -2 5,4 10 -2 5,2 10 -2 1,5 10 -3 1 8,3 8 0,4 жидкие унции (Великобритания) 1,73 10-3 3,7 10 -5 7,5 10 -3 6,45 10 -3 6,25 10 -3 1,79 10 -4 0,12 1 0,96 5 10 -2 унции жидкости (США) 1,8 10 -3 3,87 10 -5 7,8 10 -3 6,7 10 -3 6,5 10 -3 1,89 10 -4 0,13 1,04 1 0,052 пинты (Великобритания) 34,7 0,02 7,4 10 -4 0,15 0,129 0,125 3,57 10 3 2,4 20 19,2 1 Как рассчитать объем? — Формулы объема
На этот вопрос нет однозначного ответа, так как он зависит от формы рассматриваемого объекта.
 Вот формулы для некоторых наиболее распространенных форм:
Вот формулы для некоторых наиболее распространенных форм:куб =
с³, где с длина стороны.Сфера =
(4/3)πr³, где r — радиус.Цилиндр =
πr²h, где r — радиус, а h — высота.Конус =
(1/3)πr²h, где r — радиус, а h — высота.Прямоугольное тело (объем коробки) =
lwh, где l длина, w ширина и h высота (примером такой формы может служить простой бассейн).Пирамида =
(1/3) Ah, где A — площадь основания, а h — высота. Для пирамиды с правильным основанием можно использовать и другое уравнение: правильный многоугольник.Призма =
πAh, где A — площадь основания, а h — высота. Для прямой треугольной призмы уравнение можно легко вывести, как и для правильной прямоугольной призмы, которая, по-видимому, имеет ту же форму, что и коробка.
Форма Имя Формула Куб В = с³ Правая прямоугольная призма (прямоугольная, прямоугольная) В = лвч Призма или цилиндр В = Ач Пирамида или конус В = Ач/3 Сфера В = 4πr³/3 Калькулятор объема и инструменты, предназначенные для определенных форм
Мы решили сделать этот калькулятор объема простым инструментом, который охватывает пять самых популярных трехмерных форм. Однако не каждое уравнение объема и тип формы могут быть реализованы здесь, так как это сделает калькулятор перегруженным и неинтуитивным.
 Поэтому, если вы ищете конкретную форму, воспользуйтесь калькуляторами, посвященными объемам выбранных фигур:
Поэтому, если вы ищете конкретную форму, воспользуйтесь калькуляторами, посвященными объемам выбранных фигур:- Объем куба
- Объем прямоугольной призмы (коробка)
- Объем треугольной призмы
- Объем конуса
- Объем пирамиды
- Объем цилиндра
- Объем сферы
- Объем полушария
Как пользоваться калькулятором объема?
Давайте посмотрим на примере, как использовать этот калькулятор объема:
Выберите тип 3D-фигуры . Если вы не можете найти фигуру, объем которой хотите рассчитать, выберите другие специальные специальные калькуляторы (ссылки вы найдете выше). В этом примере предположим, что вы хотите вычислить объем цилиндра.
Выберите нужный раздел калькулятора объема . В нашем случае это деталь под названием Cylinder volume .
Введите данные в соответствующие поля .
 Наш цилиндр имеет радиус 1 фут и высоту 3 фута. Вы можете изменить единицы измерения, просто щелкнув имя единицы измерения.
Наш цилиндр имеет радиус 1 фут и высоту 3 фута. Вы можете изменить единицы измерения, просто щелкнув имя единицы измерения.Вот! Отображается объем выбранной формы . В нашем случае это 9,42478 кубических футов
.
Если вы хотите проверить, сколько это в баррелях США, просто нажмите на название единицы и выберите баррели из выпадающего списка. Наш цилиндр имеет вместимость ~ 2,24 барреля нефти.
Измерение объема твердых тел, жидкостей и газов
Как найти объем тел с различным агрегатным состоянием?
1. Твердое тело
Объем обычных трехмерных объектов можно легко рассчитать, измерив их размеры и применив соответствующее уравнение объема. Если это неправильная форма, вы можете попытаться сделать то же самое, что заставило Архимеда выкрикнуть знаменитое слово 9.0115 Эврика ! Вероятно, вы слышали эту историю — Архимеда попросили узнать, сделана ли корона Гиерона из чистого золота или просто позолочена, — но не сгибая и не разрушая ее.
 Идея пришла ему в голову, когда он принимал ванну — шагнув в ванну, он заметил, что уровень воды поднялся. Из этого наблюдения он сделал вывод, что объем вытесненной воды должен быть равен объему той части его тела, которую он погрузил под воду. Зная неправильный объем предмета и его вес, он мог рассчитать плотность и сравнить ее с плотностью чистого золота. Легенда гласит, что Архимед был так взволнован этим открытием, что выскочил из ванны и голым побежал по улицам Сиракуз.
Идея пришла ему в голову, когда он принимал ванну — шагнув в ванну, он заметил, что уровень воды поднялся. Из этого наблюдения он сделал вывод, что объем вытесненной воды должен быть равен объему той части его тела, которую он погрузил под воду. Зная неправильный объем предмета и его вес, он мог рассчитать плотность и сравнить ее с плотностью чистого золота. Легенда гласит, что Архимед был так взволнован этим открытием, что выскочил из ванны и голым побежал по улицам Сиракуз.Итак, если вы хотите измерить объем объекта неправильной формы, просто следуйте по стопам Архимеда (хотя вы можете опустить часть «голых гонок»):
Возьмите контейнер больше, чем объект, объем которого вы хотите измерить . Это может быть ведро, мерный стакан, химический стакан или мерный цилиндр. Он должен иметь шкалу.
Налейте воду в емкость и прочтите показания объема.
Поместите предмет внутрь .
 Он должен быть полностью погружен для измерения всего объема объектов. Прочтите объем. Этот метод не сработает, если ваш объект растворяется в воде.
Он должен быть полностью погружен для измерения всего объема объектов. Прочтите объем. Этот метод не сработает, если ваш объект растворяется в воде.Разница между измерениями и есть объем нашего объекта.
Эти измерения необходимы для расчета выталкивающей силы, основанной на принципе Архимеда.
2. Жидкость
Обычно довольно легко измерить объем жидкости — все, что вам нужно, это какой-нибудь градуированный мерный сосуд. Выберите тот, который соответствует вашим потребностям: количество жидкости и степень точности являются параметрами, которые следует учитывать. Контейнеры, используемые при выпечке торта (посмотрите замечательный калькулятор для рецепта блинов), будут отличаться от тех, которые используются в химии (например, для расчетов молярной концентрации), будут отличаться от тех, которые используются в медицинских целях (например, доза лекарства).
3. Газ
Мы должны использовать более сложные методы для измерения объема газа.
 Вы должны помнить, что на объем газа влияют температура и давление, и что газы расширяются, чтобы заполнить любой контейнер, в который они помещены. Вы можете попробовать измерить это:
Вы должны помнить, что на объем газа влияют температура и давление, и что газы расширяются, чтобы заполнить любой контейнер, в который они помещены. Вы можете попробовать измерить это:Накачайте воздушный шар газом, который вы хотите измерить (например, гелием, чтобы поднять вас в воздух). Тогда можно воспользоваться методом Архимеда — опустить шарик в ведро с водой и проверить разницу в объеме. Подробные инструкции вы найдете на странице wikihow.
Проверьте показатели объема легких с помощью устройства под названием спирометр .
В химии газовый шприц используется для введения или удаления объема газа из закрытой системы . Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.
Или вычислить :
Найдите объем газа, зная его плотность и массу .
 Используйте простое уравнение объема
Используйте простое уравнение объема V = m / d.Рассчитайте объем сжатого газа в цилиндре, используя уравнение идеального газа.
Как найти объем прямоугольника по сравнению с объемом коробки
Вы не можете вычислить объем прямоугольника , объем круга или объем квадрата, потому что они являются двумерными геометрическими фигурами. Таким образом, прямоугольник не имеет объема (но имеет площадь). То, что вы, вероятно, ищете, это объем прямоугольного параллелепипеда (или, в более общем смысле, вы хотите найти объем коробки), который является трехмерным объектом.
Чтобы найти объем коробки, просто умножьте длину, ширину и высоту — и готово! Например, если коробка 5×7×2 см, то объем коробки 70 кубических сантиметров.
Для размеров, которые представляют собой относительно небольшие целые числа, легко вычислить объем вручную. Для больших или десятичных чисел использование калькулятора объема очень эффективно.
Реальные приложения
В реальной жизни есть много приложений, где калькулятор объема полезен. Одним из таких примеров является строительство дорог или тротуаров, где необходимо соорудить бетонные плиты. Как правило, бетонные плиты представляют собой прямоугольные твердые тела, поэтому можно использовать калькулятор бетона, который является приложением к калькулятору объема.
Также формулы объема могут быть полезны, если вы увлеченный садовод или просто счастливый обладатель дома с двором. Ознакомьтесь с нашими замечательными инструментами, такими как:
Калькулятор мульчи для расчета количества мульчи, необходимого для вашего садового проекта.
Калькулятор почвы и калькулятор почвы для горшков для расчета объема и стоимости верхнего слоя почвы, а также количества почвы, необходимой для вашего цветочного горшка.
Калькулятор гравия, который может помочь в планировании строительства подъездной дороги из гравия.

Песок и песок для брусчатки, чтобы помочь вам с расчетами на строительной площадке.
Кроме того, вы можете встретить том на своей кухне или в ванной: любая жидкость, которую мы пьем (например, вода в бутылках), а также косметические средства или зубная паста имеют объем, написанный на упаковке продукта (либо в миллилитрах/литрах, либо в жидкостях). унций/галлонов).
Далее, расчеты объема очень удобны, если вы хотите гарантировать достаточное жизненное пространство для ваших любимых питомцев, будь то черепахи/рыбы, содержащиеся в аквариуме, или мыши/крысы в клетках.
Другим родственным приложением, хотя и немного отличающимся, является понятие площади поверхности. Предположим, нужно покрасить весь фасад здания. Чтобы узнать, сколько краски необходимо купить, необходимо рассчитать площадь поверхности здания. Удобный в использовании калькулятор площади поверхности рассчитает это за вас.
FAQ
Как узнать объем?
Формула объема зависит от формы объекта .
 Одной из самых популярных форм является прямоугольная призма, также известная как прямоугольник, где вы можете просто умножьте длину на ширину и высоту на , чтобы найти его объем. Другой распространенной формой является цилиндр. Чтобы найти его объем, умножьте высоту цилиндра на площадь его основания (π × r 2 ). Для других 3D-форм проверьте калькулятор объема Omni.
Одной из самых популярных форм является прямоугольная призма, также известная как прямоугольник, где вы можете просто умножьте длину на ширину и высоту на , чтобы найти его объем. Другой распространенной формой является цилиндр. Чтобы найти его объем, умножьте высоту цилиндра на площадь его основания (π × r 2 ). Для других 3D-форм проверьте калькулятор объема Omni.Как измерить объем?
Измерение объема зависит от состояния материи вашего объекта. Для жидкостей можно использовать мерный цилиндр или бюретку для измерений в химической лаборатории или мерный стакан и ложка для повседневного использования. Для газов, чтобы приблизительно измерить объем, вы можете надуть воздушный шар и использовать его для вытеснения воды в градуированном цилиндре. Аналогичный метод работает и с твердыми телами — поместите объект в градуированный контейнер и измерьте изменение показаний.
Объем в квадрате или в кубе?
Объем «в кубе» , так как это трехмерная мера.
 Площадь представляет собой квадратное значение, поскольку площадь фигуры охватывает два измерения. Вы можете вспомнить, что объем представляет собой значение в кубе, вспомнив несколько названий единиц объема, например 9.0216 кубических метров , кубических футов или кубических ярдов .
Площадь представляет собой квадратное значение, поскольку площадь фигуры охватывает два измерения. Вы можете вспомнить, что объем представляет собой значение в кубе, вспомнив несколько названий единиц объема, например 9.0216 кубических метров , кубических футов или кубических ярдов .Как рассчитать объем?
В зависимости от формы вашего объекта вы можете использовать различные формулы для расчета объема:
- Объем куба = сторона 3
- Кубовидный (прямоугольный) объем = длина × ширина × высота
- Объем сферы = (4/3) × π × радиус 3
- Объем цилиндра = π × радиус 2 × высота
- Объем конуса = (1/3) × π × радиус 2 × высота
- Объем пирамиды = (1/3) × площадь основания × высота
В чем измеряется объем?
Кубический метр — единица измерения объема в системе СИ.
 Однако, поскольку это довольно непрактично, чаще всего вы встретите объем, выраженный в:
Однако, поскольку это довольно непрактично, чаще всего вы встретите объем, выраженный в:- Кубических сантиметрах
- Кубические дюймы
- Миллилитров
- литров
- галлона
Как найти объем жидкости?
Градуированные цилиндры и Колбы Эрленмейера подойдут, если вам нужно приблизительно измерить объем жидкости. Для более точных измерений нужно использовать мерную пипетку и бюретку. Однако, если вы печете торт или готовите вкусное блюдо и в рецепте используются единицы измерения объема, вы можете просто использовать мерный стакан, стакан или ложку.
Что такое единица СИ для объема?
Метр кубический (м 3 ) — единица объема в системе СИ. Оно образовано от базовой единицы длины СИ — метра. Хотя основной единицей СИ является кубический метр, чаще используются другие единицы: для метрической системы популярны миллилитры, литры или кубические сантиметры, тогда как для имперской системы вы можете найти объем, выраженный в пинтах, галлонах, кубических дюймах, кубические футы или кубические ярды.

Является ли объем интенсивным или экстенсивным?
Объем — это экстенсивное свойство , такое же, как количество вещества, масса, энергия или энтропия. Экстенсивное свойство – это мера, которая зависит от количества материи . Посмотрите на этот пример: стакан, бочка и бассейн, наполненный водой, имеют разные объемы и массы ( экстенсивные свойства ), но вода в этих трех сосудах будет иметь одинаковую плотность, показатель преломления и вязкость ( интенсивные свойства ).
В чем разница между площадью поверхности и объемом?
Объем — это трехмерная мера , а площадь поверхности — двумерная . Объем говорит нам о кубическом пространстве, которое занимает объект, а площадь поверхности представляет собой сумму всех площадей, образующих трехмерную форму. Возьмем, к примеру, картонную коробку 📦:
- Объем — это объем пространства, занимаемый коробкой — просто пространство, доступное внутри коробки .

- Площадь поверхности — это площадь , занимаемая сторонами коробки , рассчитанная при покраске сторон или обертывании коробки бумагой.
Как найти объем объекта неправильной формы?
Вы можете использовать метод вытеснения жидкости для твердых объектов неправильной формы:
- Наполните контейнер водой и отметьте уровень воды.
- Бросьте предмет внутрь и снова отметьте уровень. Убедитесь, что ваш объект не растворяется в воде.
- Для масштабируемых контейнеров можно просто вычесть исходный том из нового тома. Вот и все, поздравляю!
Но если в исходном контейнере нет весов:
- Достаньте объект.
- Наполните контейнер водой до второй отметки, налейте эту воду в мерный цилиндр/другой мерный сосуд.
- Повторите шаг 6 для другого отмеченного уровня и вычтите объемы.

- Погладьте себя по спине — вы нашли объем объекта неправильной формы!
Что измеряет объем?
Объем измеряет объем пространства, занимаемого объектом в трех измерениях . Еще один тесно связанный с ним термин — вместимость, то есть объем внутренней части объекта. Другими словами, вместимость описывает, сколько может вместить контейнер (воды, газа и т. д.).
Каков объем Земли?
Объем Земли примерно равен 1,08321×10 12 км 3 ( 1,08 квадриллион кубических километров ), или 2,59876×10 11 кубических миль 25 триллионов кубических миль 25). Вы можете получить этот результат, используя формулу объема сферы (4/3) × π × радиус 3 и предполагая, что средний радиус Земли составляет 6371 километр (3958,76 миль).
Как рассчитать отношение площади поверхности к объему?
Чтобы рассчитать отношение площади поверхности к объему SA:V, просто разделите площадь поверхности на объем .
 Для некоторых выбранных форм:
Для некоторых выбранных форм:- Соотношение SA:V для куба = (6 × сторона 2 ) / (сторона 3 ) = 6 / сторона
- Отношение SA:V для сферы = (4 × π × радиус 2 ) / ((4/3) × π × радиус 3 )= 3 / радиус
- Отношение SA:V для цилиндра = (2 × π × радиус 2 + 2 × π × радиус × высота) / (π × радиус 2 × высота) = 2 × (радиус + высота) / (радиус × высота)
Ханна Памула, кандидат наук, Петр Малек и Матеуш Муха
Ширина (ш)
Длина (л)
Высота (в)
Объем
Ищете объем частично заполненного контейнера, например, аквариума? Тогда обязательно ознакомьтесь с нашим замечательным калькулятором объема бака!
Посмотрите 20 похожих калькуляторов 3D-геометрии 📦
Площадь полушарияCubeCube Рассчитать: найти v, a, d… Еще 17
Однократное объемное изображение образцов толстой ткани с помощью устанавливаемого одним касанием устройства для создания световой иглы
Введение
Конфокальная лазерная сканирующая микроскопия (КЛСМ) и лазерная сканирующая микроскопия с двухфотонным возбуждением (TPLSM) позволяют получать флуоресцентную визуализацию динамических молекулярных и клеточных явлений в живых образцах 1,2 .
 Из-за превосходной глубины проникновения и меньшей инвазивности из-за длины волны возбуждающего лазера в ближней инфракрасной области (БИК) по сравнению с длиной волны CLSM на основе однофотонного возбуждения, TPLSM используется для толстых биологических образцов. Для визуализации трехмерных микроструктур образцов системам обычно требуется z- методы сканирования, такие как двигатель привода фокусировки или пьезопривод для изменения относительного положения линзы объектива и образцов. Таким образом, временное разрешение для объемной визуализации в первую очередь зависит от механической скорости z -сканирования, для чего обычно требуется не менее нескольких секунд 3,4,5 . Однако для трехмерной визуализации биологических процессов в живых организмах обычно требуется значительно более высокое временное разрешение. Например, захват переходных процессов кальция и / или отслеживание динамики субклеточных структур (например, активности через дендритные шипы) в масштабе менее секунды имеет решающее значение для визуализации активности нейронов in vivo.
Из-за превосходной глубины проникновения и меньшей инвазивности из-за длины волны возбуждающего лазера в ближней инфракрасной области (БИК) по сравнению с длиной волны CLSM на основе однофотонного возбуждения, TPLSM используется для толстых биологических образцов. Для визуализации трехмерных микроструктур образцов системам обычно требуется z- методы сканирования, такие как двигатель привода фокусировки или пьезопривод для изменения относительного положения линзы объектива и образцов. Таким образом, временное разрешение для объемной визуализации в первую очередь зависит от механической скорости z -сканирования, для чего обычно требуется не менее нескольких секунд 3,4,5 . Однако для трехмерной визуализации биологических процессов в живых организмах обычно требуется значительно более высокое временное разрешение. Например, захват переходных процессов кальция и / или отслеживание динамики субклеточных структур (например, активности через дендритные шипы) в масштабе менее секунды имеет решающее значение для визуализации активности нейронов in vivo. Помимо флуоресцентной микроскопии, была разработана сложная фазовая микроскопия, такая как цифровая голографическая микроскопия, для трехмерной визуализации нефлуоресцентных биологических образцов с высоким пространственно-временным разрешением 6,7 . Такие технологии можно использовать одновременно с флуоресцентной микроскопией, позволяя накладывать флуоресцентные сигналы на трехмерные изображения. Однако, поскольку в большинстве случаев фазовая микроскопия требует проходящего света через образец для реконструкции трехмерного изображения, трудно применять крупномасштабные толстые образцы, такие как живые животные.
Помимо флуоресцентной микроскопии, была разработана сложная фазовая микроскопия, такая как цифровая голографическая микроскопия, для трехмерной визуализации нефлуоресцентных биологических образцов с высоким пространственно-временным разрешением 6,7 . Такие технологии можно использовать одновременно с флуоресцентной микроскопией, позволяя накладывать флуоресцентные сигналы на трехмерные изображения. Однако, поскольку в большинстве случаев фазовая микроскопия требует проходящего света через образец для реконструкции трехмерного изображения, трудно применять крупномасштабные толстые образцы, такие как живые животные.Для удовлетворения этих требований были предложены передовые флуоресцентные микроскопические технологии для быстрой объемной визуализации 8 . Среди них инженеры TPLSM на основе луча Бесселя, точечные функции рассеяния (PSF) для увеличения эффективной глубины резкости (DOF) 9,10,11,12 , который позволяет получать проекционные изображения путем сканирования игольчатого возбуждения, образованного лучом Бесселя в фокусе.
 Этот метод становится жизнеспособным вариантом для визуализации более крупных тканей, таких как мозг. Чтобы получить проекционное изображение с одним сканированием с помощью луча Бесселя, перед фокусировкой пространственное распределение луча возбуждающего света было преобразовано в кольцеобразную форму. В принципе, пучок кольцеобразной формы должен формироваться в плоскости зрачка объектива или в его оптически ретранслируемом положении. Однако эти идеальные положения обычно недоступны для коммерчески доступных систем TPLSM. Таким образом, реализация визуализации с помощью световой иглы в системе TPLSM требует глубокого понимания сложной оптической системы, которую необходимо модифицировать, установки дорогостоящих систем, изготовленных по индивидуальному заказу, или создания установки микроскопа с нуля. Из-за этих факторов большинству биологов трудно использовать визуализацию световой иглой в системах TPLSM.
Этот метод становится жизнеспособным вариантом для визуализации более крупных тканей, таких как мозг. Чтобы получить проекционное изображение с одним сканированием с помощью луча Бесселя, перед фокусировкой пространственное распределение луча возбуждающего света было преобразовано в кольцеобразную форму. В принципе, пучок кольцеобразной формы должен формироваться в плоскости зрачка объектива или в его оптически ретранслируемом положении. Однако эти идеальные положения обычно недоступны для коммерчески доступных систем TPLSM. Таким образом, реализация визуализации с помощью световой иглы в системе TPLSM требует глубокого понимания сложной оптической системы, которую необходимо модифицировать, установки дорогостоящих систем, изготовленных по индивидуальному заказу, или создания установки микроскопа с нуля. Из-за этих факторов большинству биологов трудно использовать визуализацию световой иглой в системах TPLSM.Здесь мы предлагаем метод получения объемных изображений с расширенной глубиной резкости в TPLSM с использованием недавно разработанного, простого в использовании устройства для создания легкой иглы, которое можно легко установить в имеющиеся в продаже микроскопические системы.
 Простое вставление устройства в одно из положений турели фильтра в вертикальном микроскопе приводит к удлинению в осевом направлении PSF более чем в 70 раз по сравнению с обычным TPLSM. Кроме того, разработанная система микроскопии успешно продемонстрировала однократную визуализацию активности кальция с временным разрешением 7,5 Гц в остром срезе мозга мыши, экспрессирующем jGCaMP7, толщиной ок. 250 мкм.
Простое вставление устройства в одно из положений турели фильтра в вертикальном микроскопе приводит к удлинению в осевом направлении PSF более чем в 70 раз по сравнению с обычным TPLSM. Кроме того, разработанная система микроскопии успешно продемонстрировала однократную визуализацию активности кальция с временным разрешением 7,5 Гц в остром срезе мозга мыши, экспрессирующем jGCaMP7, толщиной ок. 250 мкм.Результаты
Конструкция устройства для создания световой иглы и оценка эффективной глубины резкости
На рис. 1а показана схема оптической установки. Устройство создания световой иглы является ключевым компонентом для создания игольчатого пятна возбуждения в фокусе объектива в нашей системе TPLSM. Это устройство, состоящее из вогнутого аксикона и плосковыпуклой линзы, вставляется непосредственно в одно положение турели фильтра прямого микроскопа нашей системы TPLSM (рис. 1b). Вогнутый аксикон преобразует падающий гауссов пучок в кольцеобразно распространяющийся за счет преломления конической поверхностью.
Рисунок 1 Затем преобразованный пучок образует тонкую кольцеобразную структуру в фокусе выпуклой линзы, встроенной в составное устройство. В нашей установке мы использовали вогнутый аксикон с углом при вершине — 170 ° для создания луча кольцеобразной формы с внутренним диаметром примерно 12 мм в месте расположения линзы объектива. Внутренний диаметр составлял 68% зрачка объектива (17,6 мм). Плосковыпуклая линза имела фокусное расстояние 150 мм, что соответствовало физическому расстоянию между центральным положением устройства и входным положением линзы объектива. Полученный пучок кольцевой формы фокусировался линзой объектива, образуя игольчатое пятно двухфотонного возбуждения. Флуоресцентное излучение флуорофоров, находящихся в фокальном объеме, собиралось тем же объективом и отражалось дихроичным зеркалом в сторону недесканируемого детектора перед устройством создания световой иглы.
Затем преобразованный пучок образует тонкую кольцеобразную структуру в фокусе выпуклой линзы, встроенной в составное устройство. В нашей установке мы использовали вогнутый аксикон с углом при вершине — 170 ° для создания луча кольцеобразной формы с внутренним диаметром примерно 12 мм в месте расположения линзы объектива. Внутренний диаметр составлял 68% зрачка объектива (17,6 мм). Плосковыпуклая линза имела фокусное расстояние 150 мм, что соответствовало физическому расстоянию между центральным положением устройства и входным положением линзы объектива. Полученный пучок кольцевой формы фокусировался линзой объектива, образуя игольчатое пятно двухфотонного возбуждения. Флуоресцентное излучение флуорофоров, находящихся в фокальном объеме, собиралось тем же объективом и отражалось дихроичным зеркалом в сторону недесканируемого детектора перед устройством создания световой иглы.( a ) Оптическая схема разработанной световой игольчатой микроскопии.
 ( b ) Фотография устройства для создания световой иглы, помещенного в турель фильтра прямого микроскопа. ( c ) Схема генерации светового пятна для номинального падения (слева) и наклонного падения (справа) на устройство при растровом сканировании возбуждающего лазерного луча.
( b ) Фотография устройства для создания световой иглы, помещенного в турель фильтра прямого микроскопа. ( c ) Схема генерации светового пятна для номинального падения (слева) и наклонного падения (справа) на устройство при растровом сканировании возбуждающего лазерного луча.Полноразмерное изображение
В ранее описанных системах TPLSM, использующих модуляцию волнового фронта, компонент формирования луча был помещен в соответствующее положение, соответствующее зрачку объектива, с использованием передающей оптики 8,9,10,11,12 или вблизи зрачка 13,14 . Хотя использование луча Бесселя в TPLSM хорошо известно, в большинстве предыдущих работ использовалась сложная передающая оптика, а также аксикон для создания луча Бесселя 9,10 . Напротив, наше устройство, минимально состоящее из аксикона и линзы, было вставлено в положение, отличное от положения зрачка и одной прорези турели фильтра. Эта конфигурация обеспечивает замечательную простоту внедрения, однако для растрового сканирования необходимо учитывать наклон световой стрелки в зависимости от положения, как показано на рис.
 1c. Когда луч был перпендикулярен центру устройства, пятно иглы было параллельно оптической оси. Напротив, сканирование возбуждающего луча вызывало наклонное падение на устройство, в результате чего луча кольцеобразной формы с искаженным распределением интенсивности и боковым смещением на зрачке. Следовательно, ось пятна иглы была наклонена в сторону, противоположную углу падения.
1c. Когда луч был перпендикулярен центру устройства, пятно иглы было параллельно оптической оси. Напротив, сканирование возбуждающего луча вызывало наклонное падение на устройство, в результате чего луча кольцеобразной формы с искаженным распределением интенсивности и боковым смещением на зрачке. Следовательно, ось пятна иглы была наклонена в сторону, противоположную углу падения.Сначала мы измерили изображения TPLSM флуоресцентных шариков, закрепленных на покровном стекле, чтобы оценить эффективное удлинение глубины резкости, вызванное нашим устройством для создания световых игл. Во-первых, обычное изображение xyz получается без устройства, как показано на рис. 2a. Затем падающий гауссов пучок был преобразован в пучок Бесселя с помощью устройства для создания световой иглы, и тот же образец был измерен путем изменения относительного положения линзы объектива (рис. 2b). Как показано на рис. 2c, 9Изображение 2581 xy в положении 0 мкм, полученное с помощью устройства, было похоже на изображение, возбужденное гауссовым пучком, на рис.
Рисунок 2 2а, за исключением краевой области поля зрения (FOV), которая могла быть искажена кривизной поля, вызванной Устройство. Чтобы оценить расширение DOF, мы измерили сложенное изображение того же FOV для диапазона z 600 мкм. В TPLSM использовалось устройство создания световой иглы для записи изображения шарика без размытия для диапазона z , достигающего 200 мкм, что указывает на значительное расширение глубины резкости. Однако изображения TPLSM были увеличены за счет отделения от фокального положения из-за наклона PSF в зависимости от угла падающего луча (рис. 1c). Чтобы оценить взаимосвязь между коэффициентом масштабирования и расстоянием от фокуса, расстояние между двумя отдельными шариками измерялось как число пикселей на каждые z позиции. Коэффициент масштабирования был рассчитан и нанесен на график в зависимости от расстояния от фокуса путем сравнения каждого расстояния с расстоянием от сканированного по Гауссу изображения (рис. 2d). Учитывая, что угол наклона PSF линейно увеличивается с расстоянием от центра FOV, эффективный шаг пикселя уменьшается линейно от идеального шага пикселя по мере увеличения глубины наблюдения.
2а, за исключением краевой области поля зрения (FOV), которая могла быть искажена кривизной поля, вызванной Устройство. Чтобы оценить расширение DOF, мы измерили сложенное изображение того же FOV для диапазона z 600 мкм. В TPLSM использовалось устройство создания световой иглы для записи изображения шарика без размытия для диапазона z , достигающего 200 мкм, что указывает на значительное расширение глубины резкости. Однако изображения TPLSM были увеличены за счет отделения от фокального положения из-за наклона PSF в зависимости от угла падающего луча (рис. 1c). Чтобы оценить взаимосвязь между коэффициентом масштабирования и расстоянием от фокуса, расстояние между двумя отдельными шариками измерялось как число пикселей на каждые z позиции. Коэффициент масштабирования был рассчитан и нанесен на график в зависимости от расстояния от фокуса путем сравнения каждого расстояния с расстоянием от сканированного по Гауссу изображения (рис. 2d). Учитывая, что угол наклона PSF линейно увеличивается с расстоянием от центра FOV, эффективный шаг пикселя уменьшается линейно от идеального шага пикселя по мере увеличения глубины наблюдения. Другими словами, коэффициент масштабирования, определяемый как величина, обратная отношению размера эффективного поля зрения к идеальному, был обратно пропорционален глубине (синяя кривая подгонки на рис. 2d). Длину созданной световой иглы оценивали по аксиальному профилю интенсивности флуоресценции, показанному на рис. 2e. Поскольку форма осевого профиля интенсивности была асимметрична положению максимальной интенсивности, полная ширина на полувысоте (FWHM) определялась расстоянием между двумя точками полумаксимума, каждая из которых была получена из линии приблизительно 7 точек данных вокруг половины максимума интенсивности флуоресценции, что соответствовало диапазону 15 мкм, и подтвердили, что FWHM составляла 144 мкм. Это значение ясно указывает на заметное расширение DOF, соответствующее более чем 70-кратному осевому размеру PSF, определенному при визуализации 0,2-мкм флуоресцентной бусины без устройства.
Другими словами, коэффициент масштабирования, определяемый как величина, обратная отношению размера эффективного поля зрения к идеальному, был обратно пропорционален глубине (синяя кривая подгонки на рис. 2d). Длину созданной световой иглы оценивали по аксиальному профилю интенсивности флуоресценции, показанному на рис. 2e. Поскольку форма осевого профиля интенсивности была асимметрична положению максимальной интенсивности, полная ширина на полувысоте (FWHM) определялась расстоянием между двумя точками полумаксимума, каждая из которых была получена из линии приблизительно 7 точек данных вокруг половины максимума интенсивности флуоресценции, что соответствовало диапазону 15 мкм, и подтвердили, что FWHM составляла 144 мкм. Это значение ясно указывает на заметное расширение DOF, соответствующее более чем 70-кратному осевому размеру PSF, определенному при визуализации 0,2-мкм флуоресцентной бусины без устройства.TPLSM-изображения флуоресцентно меченых шариков на покровном стекле.
 ( a ) Xy изображение в фокусе ( z = 0 мкм) и реконструированное изображение xz из стопок z- (толщиной 30 мкм), измеренных с помощью гауссова пучка. ( b ) Относительные конфигурации объектива и образца. ( c ) Xy изображение в фокусе, на расстоянии 100 и 200 мкм от фокуса и реконструированное xz изображение из z- стопки (толщиной 600 мкм), измеренные лучом Бесселя, созданным устройством создания световой иглы. На вставках показаны профили интенсивности флуоресценции вдоль красных линий на изображениях xy . Масштабные полосы вдоль xy изображений были показаны как их пиксели. ( d ) Эффект масштабирования изображений, отсканированных лучом Бесселя, в зависимости от положения от фокуса. ( e ) Осевой профиль интенсивности флуоресценции изображения TPLSM, измеренный лучом Бесселя.
( a ) Xy изображение в фокусе ( z = 0 мкм) и реконструированное изображение xz из стопок z- (толщиной 30 мкм), измеренных с помощью гауссова пучка. ( b ) Относительные конфигурации объектива и образца. ( c ) Xy изображение в фокусе, на расстоянии 100 и 200 мкм от фокуса и реконструированное xz изображение из z- стопки (толщиной 600 мкм), измеренные лучом Бесселя, созданным устройством создания световой иглы. На вставках показаны профили интенсивности флуоресценции вдоль красных линий на изображениях xy . Масштабные полосы вдоль xy изображений были показаны как их пиксели. ( d ) Эффект масштабирования изображений, отсканированных лучом Бесселя, в зависимости от положения от фокуса. ( e ) Осевой профиль интенсивности флуоресценции изображения TPLSM, измеренный лучом Бесселя.Полноразмерное изображение
Визуализация тонкой структуры очищенных срезов головного мозга с помощью устройства для создания световой иглы
После характеристики эффективной глубины резкости с помощью измерений флуоресцентных шариков мы подтвердили эффективность нашего метода объемной визуализации в биологических образцах.
Рисунок 3 Корональный срез мозга мыши Thy1-YFP-H, содержащий сенсорную кору, фиксировали и обрабатывали очищающим раствором Sca l eA2. Sca l eA2 — это водный реагент, очищающий фиксированную биологическую ткань без гашения флуоресцентных сигналов, а также уменьшающий светорассеяние в толстых образцах 15 . Сначала было получено изображение xyz по всему образцу толщиной 250 мкм с использованием обычного сканирования гауссовым лучом, а относительная конфигурация объектива и фиксированного среза показана на рис. 3a. Затем было получено одно изображение x y с использованием сканирования луча Бесселя, созданного нашим устройством для создания световой иглы. Сома и нейриты на лучевом изображении Бесселя легко идентифицируются, и их глубину можно реконструировать, сравнивая ее с проекционным изображением максимальной интенсивности z — пакетное сканирование гауссовым лучом (рис. 3b, c). Как показано на рис. 3c, сома, расположенная глубоко в срезе, была увеличена (например, клетка номер 10), тогда как сома вблизи поверхности среза (например, клетка номер 1) выглядела похожей на изображение, возбужденное гауссовым лучом.
Корональный срез мозга мыши Thy1-YFP-H, содержащий сенсорную кору, фиксировали и обрабатывали очищающим раствором Sca l eA2. Sca l eA2 — это водный реагент, очищающий фиксированную биологическую ткань без гашения флуоресцентных сигналов, а также уменьшающий светорассеяние в толстых образцах 15 . Сначала было получено изображение xyz по всему образцу толщиной 250 мкм с использованием обычного сканирования гауссовым лучом, а относительная конфигурация объектива и фиксированного среза показана на рис. 3a. Затем было получено одно изображение x y с использованием сканирования луча Бесселя, созданного нашим устройством для создания световой иглы. Сома и нейриты на лучевом изображении Бесселя легко идентифицируются, и их глубину можно реконструировать, сравнивая ее с проекционным изображением максимальной интенсивности z — пакетное сканирование гауссовым лучом (рис. 3b, c). Как показано на рис. 3c, сома, расположенная глубоко в срезе, была увеличена (например, клетка номер 10), тогда как сома вблизи поверхности среза (например, клетка номер 1) выглядела похожей на изображение, возбужденное гауссовым лучом. Это наблюдение предполагало, что аналогичный эффект масштабирования, зависящий от глубины, возникал при сканировании лучом Бесселя, как это наблюдалось на изображении шарика (рис. 2). Чтобы подтвердить это явление (дополнительный рис. S1a), мы преобразовали исходный гауссовский z — наложили на проекционное изображение усредненной интенсивности и обработали его с помощью собственного подключаемого модуля ImageJ с учетом эффекта масштабирования, зависящего от глубины (рис. 2e). Восстановленное гауссово изображение больше соответствовало изображению луча Бесселя xy , за исключением краевой области фиксированного среза (дополнительный рис. S1b – e), которая могла быть искажена кривизной поля, вызванной устройством. Хотя это дополнительное искажение следует учитывать для реконструкции более точных изображений, такие реконструкции будут полезны для отнесения цели в более сложную и/или более плотную структуру. Как показано в этом эксперименте, мы получили объемное изображение с тонкими структурами в толстых, чистых, фиксированных срезах мозга, используя наше устройство для создания световой иглы.
Это наблюдение предполагало, что аналогичный эффект масштабирования, зависящий от глубины, возникал при сканировании лучом Бесселя, как это наблюдалось на изображении шарика (рис. 2). Чтобы подтвердить это явление (дополнительный рис. S1a), мы преобразовали исходный гауссовский z — наложили на проекционное изображение усредненной интенсивности и обработали его с помощью собственного подключаемого модуля ImageJ с учетом эффекта масштабирования, зависящего от глубины (рис. 2e). Восстановленное гауссово изображение больше соответствовало изображению луча Бесселя xy , за исключением краевой области фиксированного среза (дополнительный рис. S1b – e), которая могла быть искажена кривизной поля, вызванной устройством. Хотя это дополнительное искажение следует учитывать для реконструкции более точных изображений, такие реконструкции будут полезны для отнесения цели в более сложную и/или более плотную структуру. Как показано в этом эксперименте, мы получили объемное изображение с тонкими структурами в толстых, чистых, фиксированных срезах мозга, используя наше устройство для создания световой иглы.
Сравнение между z- сканированным изображением, полученным с помощью пучка Гаусса, и изображением, сканированным лучом Бесселя, среза мозга мыши Sca l eA2, очищенного от thy1-YFP-H. ( a ) Относительные конфигурации объектива и фиксированного среза. ( b ) Трехмерное реконструированное изображение из проекции максимальной интенсивности стека z- толщиной 250 мкм изображения нейронов (с цветовой кодировкой по глубине) в сенсорной коре, измеренной с помощью сканирования гауссовым лучом. Нейроны были последовательно пронумерованы в соответствии с z позиция начиналась с поверхности среза мозга. ( c ) Изображение xy того же поля зрения в ( b ) в фокусе, на расстоянии 60 мкм от поверхности среза, было получено путем сканирования луча Бесселя с использованием устройства создания световой иглы. Те же нейроны были выбраны и пронумерованы, как в ( b ). Масштабная линейка вдоль изображения была показана как их пиксели.

Полноразмерное изображение
Покадровая объемная визуализация динамики нейронов в острых срезах
Чтобы продемонстрировать применимость нашего метода объемной визуализации в живых организмах, мы применили этот метод к визуализации кальция в острых срезах головного мозга взрослого человека. Для этой цели экспрессирующие соматостатин (SST + ) интернейроны в медиальной префронтальной коре (mFPC) мышей SST-cre 16 были помечены Cre-индуцируемым аденоассоциированным вирусом (AAV), кодирующим индикатор кальция jGCaMP7s. Одновременно мы экспрессировали hM3Dq, сконструированный человеческий мускариновый рецептор, в той же области для искусственной и селективной активации SST 9.0234 + интернейроны, использующие дизайнерские рецепторы, активируемые исключительно дизайнерскими лекарствами (DREADD) 17 (рис. 4а). Через три недели после инъекции вируса острые срезы головного мозга, содержащие mPFC, помещали под микроскоп TPLSM. Затем мы выполнили запись сканирования луча Бесселя xy , представив наше устройство для создания световой иглы.
Рисунок 4 Клозапин-N-оксид (CNO) вводили в срезы через инфузионную систему во время сканирования лучом Бесселя для химической активации SST + 9.0235 нейронов в течение двух минут (рис. 4b). Активность кальция регистрировали до, во время и после введения CNO. В конце экспериментов та же область, полученная сканированием луча Бесселя, была затем захвачена 250-мкм z -суммированным изображением сканирования гауссовым лучом (рис. 4c-слева). Типичные примеры нейронов показаны на рис. 4d. Подобно результатам для фиксированных срезов мозга, реконструированное проекционное изображение средней интенсивности z- сложенного сканированного изображения гауссовского луча было аналогично изображению, сканированному лучом Бесселя (дополнительный рисунок S1f-i). JGGaMP7, экспрессирующие SST + интернейронов, распределенных на разной глубине, были идентифицированы по записи, возбужденной лучом Бесселя, и их расположение было определено с помощью гауссовского изображения стека z- (рис.
Клозапин-N-оксид (CNO) вводили в срезы через инфузионную систему во время сканирования лучом Бесселя для химической активации SST + 9.0235 нейронов в течение двух минут (рис. 4b). Активность кальция регистрировали до, во время и после введения CNO. В конце экспериментов та же область, полученная сканированием луча Бесселя, была затем захвачена 250-мкм z -суммированным изображением сканирования гауссовым лучом (рис. 4c-слева). Типичные примеры нейронов показаны на рис. 4d. Подобно результатам для фиксированных срезов мозга, реконструированное проекционное изображение средней интенсивности z- сложенного сканированного изображения гауссовского луча было аналогично изображению, сканированному лучом Бесселя (дополнительный рисунок S1f-i). JGGaMP7, экспрессирующие SST + интернейронов, распределенных на разной глубине, были идентифицированы по записи, возбужденной лучом Бесселя, и их расположение было определено с помощью гауссовского изображения стека z- (рис. 4c).
4c).Визуализация срезов головного мозга мышей с использованием кальция. ( a ) Стратегия инъекции вируса для экспрессии кальциевых зондов и хемогенетических инструментов в интернейронах SST + в префронтальной коре мышей SST-cre. ( b ) Хронология визуализации кальция и хемогенетических манипуляций. ( c ) Сравнение между z- суммированным сканированным изображением гауссового луча и сканированным изображением луча Бесселя. (слева) 3D-реконструированное изображение из проекции максимальной интенсивности изображения стека z- толщиной 250 мкм нейронов SST + (с цветовой кодировкой по глубине), измеренного с помощью сканирования гауссовым лучом. Нейроны были последовательно пронумерованы в порядке глубины от поверхности среза. (справа) Проекция средней интенсивности, полученная на основе данных цейтраферной съемки. Такое же поле зрения (слева) было получено на расстоянии 60 мкм от поверхности среза с помощью луча Бесселя с использованием устройства для создания световой иглы.
 Те же нейроны были пронумерованы как в (слева). Масштабная линейка вдоль изображения (слева) была показана как их пиксели. ( d ) Спонтанные и стимулированные кальциевые следы отдельных нейронов, пронумерованных ( c ), до, во время и после инфузии CNO. Увеличенные кривые показали репрезентативные события, связанные с кальцием.
Те же нейроны были пронумерованы как в (слева). Масштабная линейка вдоль изображения (слева) была показана как их пиксели. ( d ) Спонтанные и стимулированные кальциевые следы отдельных нейронов, пронумерованных ( c ), до, во время и после инфузии CNO. Увеличенные кривые показали репрезентативные события, связанные с кальцием.Изображение в натуральную величину
Используя записи сканирования пучком Бесселя, мы обнаружили, что интернейроны SST + имеют различные паттерны спонтанной кальциевой активности и ответы на хемогенетические манипуляции (рис. 4d). Некоторые нейроны показали (1) быстрые переходные процессы кальция (клетки 1 и 10), (2) колебания кальция (клетки 7) и (3) устойчивые базовые изменения (клетки 6, 8 и 9).). В большинстве нейронов также наблюдались смешанные типы кальциевой активности (например, клетки 2, 4 и 5). Гетерогенные ответы интернейронов SST + на хемогенетические манипуляции могут соответствовать недавним исследованиям, в которых интернейроны SST + обнаруживали различные биологические свойства 18,19 .

В заключение, мы успешно продемонстрировали, что сканирование луча Бесселя с использованием нашего устройства для создания световых игл позволяет отслеживать и обнаруживать различные активности популяции нейронов, расположенных в толстых образцах.
Обсуждения
В этом исследовании мы успешно продемонстрировали, что быстрые трехмерные биологические явления можно зафиксировать с помощью одного изображения xy , установив наше простое в использовании устройство для создания световой иглы на обычной системе микроскопа TPLSM (рис. 1). В частности, мы успешно визуализировали спонтанную активность до введения CNO и вызванную активность после стимуляции CNO с помощью сканирования пучком Бесселя с использованием острых срезов из SST + 9.0235-cre мышей, у которых только интернейроны SST + экспрессировали jGCaMP7s и DREADD (рис. 4). Интернейроны SST + составляют 20–30% ГАМКергических интернейронов в mPFC. Соматы интернейронов SST + в основном расположены в слоях V и II/III с плотной разветвленностью аксонов в слое I 18,19 .
 Интернейроны SST + имеют различные подгруппы с различными молекулярными профилями, анатомическими особенностями и электрофизиологическими свойствами 16 . Наша система показала способность отслеживать SST + промежуточных нейронов, распределенных на разной глубине с различными свойствами активности из большого объема (рис. 4), что согласуется с предыдущими исследованиями, что делает его мощным инструментом для выяснения того, как различные подтипы нейронов реагируют и интегрируются друг с другом при получении входных данных. сигналы из других областей мозга. Поскольку получение динамики нейронной активности в популяции нейронов с высоким пространственным и временным разрешением имеет решающее значение, предлагаемые здесь методы объемной визуализации могут преодолеть ограничения обычной микроскопии для выяснения обработки информации в нейронных схемах.
Интернейроны SST + имеют различные подгруппы с различными молекулярными профилями, анатомическими особенностями и электрофизиологическими свойствами 16 . Наша система показала способность отслеживать SST + промежуточных нейронов, распределенных на разной глубине с различными свойствами активности из большого объема (рис. 4), что согласуется с предыдущими исследованиями, что делает его мощным инструментом для выяснения того, как различные подтипы нейронов реагируют и интегрируются друг с другом при получении входных данных. сигналы из других областей мозга. Поскольку получение динамики нейронной активности в популяции нейронов с высоким пространственным и временным разрешением имеет решающее значение, предлагаемые здесь методы объемной визуализации могут преодолеть ограничения обычной микроскопии для выяснения обработки информации в нейронных схемах.Однако с точки зрения простоты использования предложенная нами методика имеет некоторые практические ограничения.
 Сначала визуализируемая цель масштабировалась на реальном изображении в зависимости от ее положения относительно линзы объектива. Кроме того, на полученное изображение повлияла сильная кривизна поля, в результате чего в центре изображения появлялась кольцеобразная тень, когда мы приближали объектив к образцам. Эти эффекты были вызваны положением создания луча Бесселя, которое не являлось сопряженной плоскостью зрачка объектива в системе. Хотя эффекты кривизны поля остались в реконструированном изображении, такая информация должна помочь определить цели для трассировки. Как показано на рис. 2c, полученная кривая коэффициента масштабирования точно соответствовала обратной линейной функции. Эта информация позволяет нам реконструировать проекционное изображение из 9Изображение 2581 xyz , полученное с использованием гауссова луча, которое почти идентично нашему одиночному сканированному лучом Бесселя изображению, как показано на дополнительном рисунке S1. С другой стороны, наклонный луч Бесселя применялся в стереоскопии, позволяя реконструировать трехмерные изображения 20 .
Сначала визуализируемая цель масштабировалась на реальном изображении в зависимости от ее положения относительно линзы объектива. Кроме того, на полученное изображение повлияла сильная кривизна поля, в результате чего в центре изображения появлялась кольцеобразная тень, когда мы приближали объектив к образцам. Эти эффекты были вызваны положением создания луча Бесселя, которое не являлось сопряженной плоскостью зрачка объектива в системе. Хотя эффекты кривизны поля остались в реконструированном изображении, такая информация должна помочь определить цели для трассировки. Как показано на рис. 2c, полученная кривая коэффициента масштабирования точно соответствовала обратной линейной функции. Эта информация позволяет нам реконструировать проекционное изображение из 9Изображение 2581 xyz , полученное с использованием гауссова луча, которое почти идентично нашему одиночному сканированному лучом Бесселя изображению, как показано на дополнительном рисунке S1. С другой стороны, наклонный луч Бесселя применялся в стереоскопии, позволяя реконструировать трехмерные изображения 20 . Аналогично, как показано на рис. 3c и 4c, флуоресцентные сигналы от сомы одинакового размера были спроецированы в нашем изображении, сканированном лучом Бесселя, как видимость размера, зависящего от глубины. В таких случаях осевое положение каждой сомы можно оценить без использования 9Изображение 2581 xyz , полученное с использованием гауссового луча, который используется в большинстве TPLSM на основе луча Бесселя 9,10,11 . Кроме того, пучок Бесселя преобразовывался из падающего гауссова луча с помощью устройства создания световой иглы в положении фильтрующего куба и вводился в зрачок объектива с расходимостью луча примерно 4,6°. Такое расхождение луча смещает осевое положение фокуса PSF от фокуса гауссова луча и может привести к снижению эффективности обнаружения флуоресцентного сигнала. Для распараллеливания луча или уменьшения угла расходимости в устройстве создания световой иглы требуются дополнительные оптические элементы. Поскольку наше устройство было спроектировано таким образом, чтобы поместиться на месте фильтрующего куба обычного микроскопа, большую часть его пространства занимала сложенная пара вогнутого аксикона и плосковыпуклой линзы.
Аналогично, как показано на рис. 3c и 4c, флуоресцентные сигналы от сомы одинакового размера были спроецированы в нашем изображении, сканированном лучом Бесселя, как видимость размера, зависящего от глубины. В таких случаях осевое положение каждой сомы можно оценить без использования 9Изображение 2581 xyz , полученное с использованием гауссового луча, который используется в большинстве TPLSM на основе луча Бесселя 9,10,11 . Кроме того, пучок Бесселя преобразовывался из падающего гауссова луча с помощью устройства создания световой иглы в положении фильтрующего куба и вводился в зрачок объектива с расходимостью луча примерно 4,6°. Такое расхождение луча смещает осевое положение фокуса PSF от фокуса гауссова луча и может привести к снижению эффективности обнаружения флуоресцентного сигнала. Для распараллеливания луча или уменьшения угла расходимости в устройстве создания световой иглы требуются дополнительные оптические элементы. Поскольку наше устройство было спроектировано таким образом, чтобы поместиться на месте фильтрующего куба обычного микроскопа, большую часть его пространства занимала сложенная пара вогнутого аксикона и плосковыпуклой линзы. Принимая это во внимание, устройства следующего поколения, использующие более тонкие элементы, такие как дифракционные оптические элементы 21 , может быть разработан для получения более ярких и простых в использовании объемных изображений.
Принимая это во внимание, устройства следующего поколения, использующие более тонкие элементы, такие как дифракционные оптические элементы 21 , может быть разработан для получения более ярких и простых в использовании объемных изображений.Наконец, благодаря простоте нашего устройства для создания световых игл его можно широко использовать для трехмерного изображения. Поскольку мы успешно расширили глубину резкости более чем на 200 мкм, это помогает получать объемные изображения значительно более крупных образцов, например, при измерении активности нейронов в мозге приматов. Более того, применение нашего устройства не ограничивается измерением сигнала кальция. Любая структура, слабо помеченная биосенсором, может быть визуализирована, и ее биологическая динамика может отслеживаться с использованием этого подхода, например, путем регистрации быстрых изменений мембранных потенциалов с помощью датчиков напряжения среди большой популяции нейронов с разрешением одной клетки.
 Использование нашего устройства с более высокой мощностью лазера в будущем также обещает визуализацию крошечных структур, таких как нейропили на рис. 4, что гарантирует нам отслеживание перемещения сигнальных молекул в нескольких дендритных шипах во время долгосрочной пластичности или поведения животных. Напротив, применение бесселевского сканирования лучом обычно требует сбора большого количества оптических компонентов и сложной установки для выстраивания всех частей в правильном порядке. Поэтому при построении системы обычно учитывается больший размер рабочего пространства, что затрудняет применение в обычной лаборатории. Наше устройство преодолело это ограничение, и его можно легко переносить в ограниченное пространство, например, в чистую комнату в больнице. Он расширяет возможности имплантации изображений на основе луча Бесселя для клинических исследований, облегчая трехмерное конструирование раковой ткани и метастазов опухоли.
Использование нашего устройства с более высокой мощностью лазера в будущем также обещает визуализацию крошечных структур, таких как нейропили на рис. 4, что гарантирует нам отслеживание перемещения сигнальных молекул в нескольких дендритных шипах во время долгосрочной пластичности или поведения животных. Напротив, применение бесселевского сканирования лучом обычно требует сбора большого количества оптических компонентов и сложной установки для выстраивания всех частей в правильном порядке. Поэтому при построении системы обычно учитывается больший размер рабочего пространства, что затрудняет применение в обычной лаборатории. Наше устройство преодолело это ограничение, и его можно легко переносить в ограниченное пространство, например, в чистую комнату в больнице. Он расширяет возможности имплантации изображений на основе луча Бесселя для клинических исследований, облегчая трехмерное конструирование раковой ткани и метастазов опухоли.В совокупности наше устройство для создания световых игл потенциально снижает стоимость и сложность объемной техники на основе сканирования луча Бесселя для более широкого применения.

Материалы и методы
Оптическая установка
Устройство для создания световой иглы состояло из изготовленного на заказ вогнутого аксикона (физический угол = − 170°; Natsume Optical Corp., Иида, Япония) и плосковыпуклой линзы ( f = 150 мм; LA1433-B, Thorlabs, Inc., Ньютон, Нью-Джерси), и был вставлен в одно положение турели фильтра вертикального микроскопа (FN-1, Nikon, Токио, Япония). Все флуоресцентные изображения были получены с использованием системы TPLSM (A1R-MP+, Nikon) с водно-иммерсионным объективом (Nikon, Apo LWD 25×/1,10 NA). Титан-сапфировый лазер (MaiTai eHP DeepSee, Spectra-Physics, Санта-Клара, Калифорния; перестраиваемая длина волны: 690–1040 нм, средняя мощность: 1,7 Вт на 920 нм, 1,3 Вт на 950 нм; ширина импульса: 100 фс, частота повторения: 80 МГц) использовали в качестве возбуждающего лазерного источника света на длинах волн 920 нм для GCaMP7 и 950 нм для EYFP. Все сигналы флуоресценции при длине волны 690 нм были обнаружены детекторами без десканирования, оснащенными GaAsP-ФЭУ (NDD).
 Чувствительность НДД и мощность лазера регулировались в соответствии с экспериментами.
Чувствительность НДД и мощность лазера регулировались в соответствии с экспериментами.Животное
Все исследования на животных проводились в соответствии с рекомендациями ARRIVE, а все процедуры по уходу за животными и экспериментальные процедуры были одобрены Институциональным комитетом по уходу и использованию животных Национального института естественных наук и проводились в соответствии с рекомендациями Национального института естественных наук. Институт физиологических наук (Одобрение № 20А017 и 20А122). Мышей содержали при температуре 22–24 °C со стандартным 12-часовым циклом свет-темнота, свободным доступом к воде и стандартным кормом. Мышиная линия Thy1-YFP-H, охарактеризованная ранее 22 , использовали для приготовления очищающих фиксирующих срезов Sca l eA2. Мышей Sst-IRES-Cre (SOM-cre) в возрасте от четырех до пяти месяцев (инвентарный номер: 013044) использовали для записи острых срезов.
Подготовка образцов шариков
Флуоресцентно меченные шарики (желто-зеленый, диаметр 0,2 мкм/нильский красный, диаметр 1 мкм; Thermo Fisher Scientific, Waltham, MA) разводили в воде (1:3000, об.
 /об.), наносили по каплям на покровное стекло и дают высохнуть. Покровные стекла монтировали с использованием монтажной среды.
/об.), наносили по каплям на покровное стекло и дают высохнуть. Покровные стекла монтировали с использованием монтажной среды.Приготовление очищающих фиксирующих срезов ScaleA2
Очищающие срезы Sca l eA2 были приготовлены, как сообщалось ранее 15 . Вкратце, мышам Thy1-YFP-H транскардиально перфузировали физиологический раствор, а затем 4% параформальдегид (PFA, в 0,1 М PB). Мозг удаляли и подвергали последующей фиксации в 4% PFA (в 0,1 M PB) при 4 °C в течение ночи; затем заменили 4% PFA на 0,1 М PB. Срезы мозга толщиной 250 мкм, содержащие соматосенсорную кору, собирали в коронарной плоскости с помощью вибратома (700smz, Campden Instruments, Лестершир, Великобритания) и инкубировали с Sca 9.2581 мкл раствора eA2 (4 М мочевины, 10 % (вес/объем) глицерина и 0,1 % (вес/объем) Triton X-100) при 37 °C в течение двух дней. Срезы помещали на предметное стекло (0,17 мм) с раствором Sca l eA2 и визуализировали с помощью системы TPLSM.
Стереотаксические вирусные инъекции
Смесь вируса AAV1-hSyn-FLEX-jGCaMP7s (104491, Addgene, Watertown, MA; 1 × 10 13 г/мл) и AAV1-hSyn-DIO-hM3Dq-mCherry, (4433 Addgene; 7 × 10 12 гв/мл) вводили односторонне в медиальную префронтальную кору (mPFC).
 Гомозиготных самок или самцов мышей Sst-IRES-Cre (возраст 3–4 месяца) анестезировали изофлураном и помещали в стереотаксический аппарат (RWD Life Science, Сан-Диего, Калифорния). После стерилизации места разреза этанолом и йодом череп обнажали и над mPFC делали небольшое отверстие. 250 нл смешанных вирусов (соотношение 1:1) вводили с использованием 10 мкл шприцев NanoFil с иглой 33 размера (NF33BV, World Precision Instruments, Сарасота, Флорида) и шприцевого насоса (Micro4, World Precision Instruments) со скоростью 10 нл/мин. в mPFC (от брегмы, переднезадний: + 2,4 мм; медиолатеральный: 0,3 мм; дорзовентральный: — 1,6 мм). Иглу медленно удаляли через 10 минут после инъекции, чтобы свести к минимуму обратный поток вируса. Мышей возвращали в их домашнюю клетку по крайней мере на три недели для восстановления перед изображением острого среза.
Гомозиготных самок или самцов мышей Sst-IRES-Cre (возраст 3–4 месяца) анестезировали изофлураном и помещали в стереотаксический аппарат (RWD Life Science, Сан-Диего, Калифорния). После стерилизации места разреза этанолом и йодом череп обнажали и над mPFC делали небольшое отверстие. 250 нл смешанных вирусов (соотношение 1:1) вводили с использованием 10 мкл шприцев NanoFil с иглой 33 размера (NF33BV, World Precision Instruments, Сарасота, Флорида) и шприцевого насоса (Micro4, World Precision Instruments) со скоростью 10 нл/мин. в mPFC (от брегмы, переднезадний: + 2,4 мм; медиолатеральный: 0,3 мм; дорзовентральный: — 1,6 мм). Иглу медленно удаляли через 10 минут после инъекции, чтобы свести к минимуму обратный поток вируса. Мышей возвращали в их домашнюю клетку по крайней мере на три недели для восстановления перед изображением острого среза.Подготовка острых срезов
Мы использовали мышей SST-Cre в возрасте 4–5 месяцев, и острые коронарные срезы головного мозга, содержащие медиальную префронтальную кору, готовили в соответствии с процедурами, описанными в предыдущем исследовании 23 .
 Вкратце, мышей глубоко анестезировали изофлураном и транскраниально перфузировали предварительно охлажденным NMDG-HEPES aCSF: 92 мМ NMDG, 2,5 мМ KCl, 1,25 мМ NaH 2 PO 4 , 30 мМ NaHCO 3 9062 м, HES 9062 2 мМ тиомочевины, 5 мМ аскорбата натрия, 3 мМ пирувата натрия, 0,5 мМ CaCl 2 , 10 мМ MgSO 4 · 7H 2 O и 25 мМ глюкозы, насыщали кислородом и доводили до pH 7,4. После декапитации мозг быстро вырезали и погружали в холодный оксигенированный NMDG-HEPES aCSF. Мозг обрезали и приклеивали к охлажденной платформе вибратома (VT1200, Leica, Nussloch, Германия). Коронарные срезы (250 мкм), содержащие mPFC, вырезали в охлажденном льдом NMDG-HEPES aCSF и непрерывно барботировали 95% O 2 и 5% CO 2 . Срезы переносили в камеру для выдержки с предварительно теплым (34 °C) оксигенированным NMDG-HEPES aCSF, и немедленно проводили процедуру защитного восстановления NMDG. При этом указанные объемы Na + вводимый раствор (2 М NaCl) добавляли в указанные моменты времени, как описано ранее 24 , для постепенного повторного введения Na + в камеру среза мозга.
Вкратце, мышей глубоко анестезировали изофлураном и транскраниально перфузировали предварительно охлажденным NMDG-HEPES aCSF: 92 мМ NMDG, 2,5 мМ KCl, 1,25 мМ NaH 2 PO 4 , 30 мМ NaHCO 3 9062 м, HES 9062 2 мМ тиомочевины, 5 мМ аскорбата натрия, 3 мМ пирувата натрия, 0,5 мМ CaCl 2 , 10 мМ MgSO 4 · 7H 2 O и 25 мМ глюкозы, насыщали кислородом и доводили до pH 7,4. После декапитации мозг быстро вырезали и погружали в холодный оксигенированный NMDG-HEPES aCSF. Мозг обрезали и приклеивали к охлажденной платформе вибратома (VT1200, Leica, Nussloch, Германия). Коронарные срезы (250 мкм), содержащие mPFC, вырезали в охлажденном льдом NMDG-HEPES aCSF и непрерывно барботировали 95% O 2 и 5% CO 2 . Срезы переносили в камеру для выдержки с предварительно теплым (34 °C) оксигенированным NMDG-HEPES aCSF, и немедленно проводили процедуру защитного восстановления NMDG. При этом указанные объемы Na + вводимый раствор (2 М NaCl) добавляли в указанные моменты времени, как описано ранее 24 , для постепенного повторного введения Na + в камеру среза мозга. Через 30 минут срезы переносили в камеру для хранения, содержащую оксигенированный HEPES, содержащий aCSF при комнатной температуре: 92 мМ NaCl, 2,5 мМ KCl, 1,25 мМ NaH 2 PO 4 , 20 мМ HEPES, 20 мМ NaHCO 3 , 2 мМ тиомочевины, 5 мМ аскорбата натрия, 3 мМ пирувата натрия, 2 мМ CaCl 2 , 2 мМ MgSO 4 ·7H 2 O и 25 мМ глюкозы титровали и доводили pH до 7,4. Срезы оставляли восстанавливаться в течение по крайней мере часа в камере для хранения перед началом записи срезов. Записи проводились при комнатной температуре (22–23 °C) с постоянной суперфузией (3 мл/мин) оксигенированного для записи aCSF: 105 мМ NaCl, 2,5 мМ KCl, 1,25 мМ NaH 2 PO 4 , 24 мМ NaHCO 3 , 2 мМ CaCl 2 · 4H 2 O, 2 мМ MgSO 4 · 7H 2 O, 12,5 мМ глюкозы и pH доведен до 7,4.
Через 30 минут срезы переносили в камеру для хранения, содержащую оксигенированный HEPES, содержащий aCSF при комнатной температуре: 92 мМ NaCl, 2,5 мМ KCl, 1,25 мМ NaH 2 PO 4 , 20 мМ HEPES, 20 мМ NaHCO 3 , 2 мМ тиомочевины, 5 мМ аскорбата натрия, 3 мМ пирувата натрия, 2 мМ CaCl 2 , 2 мМ MgSO 4 ·7H 2 O и 25 мМ глюкозы титровали и доводили pH до 7,4. Срезы оставляли восстанавливаться в течение по крайней мере часа в камере для хранения перед началом записи срезов. Записи проводились при комнатной температуре (22–23 °C) с постоянной суперфузией (3 мл/мин) оксигенированного для записи aCSF: 105 мМ NaCl, 2,5 мМ KCl, 1,25 мМ NaH 2 PO 4 , 24 мМ NaHCO 3 , 2 мМ CaCl 2 · 4H 2 O, 2 мМ MgSO 4 · 7H 2 O, 12,5 мМ глюкозы и pH доведен до 7,4.Получение изображений и анализ данных
Изображения флуоресцентных шариков, измеренные с помощью гауссова пучка, имели размер пикселя 199 нм (без биннинга), размер FOV 102 × 102 мкм (512 × 512 пикселей) и время экспозиции 1 с.
 Стопка z- (толщиной 30 мкм) была захвачена с интервалом 0,5 мкм. Для измерений одного и того же образца с помощью бесселева пучка количество пикселей, диапазон сканирования сканирующих зеркал и время экспозиции сохранялись с помощью гауссовой диаграммы, в то время как 9Стек 2581 z- (толщиной 600 мкм) был захвачен с интервалами 2,5 мкм и 10 мкм для оценки длины созданной световой иглы и эффекта масштабирования соответственно.
Стопка z- (толщиной 30 мкм) была захвачена с интервалом 0,5 мкм. Для измерений одного и того же образца с помощью бесселева пучка количество пикселей, диапазон сканирования сканирующих зеркал и время экспозиции сохранялись с помощью гауссовой диаграммы, в то время как 9Стек 2581 z- (толщиной 600 мкм) был захвачен с интервалами 2,5 мкм и 10 мкм для оценки длины созданной световой иглы и эффекта масштабирования соответственно.Изображения очищающих срезов Sca l eA2 были созданы путем усреднения двух изображений, полученных для сканирования гауссовым лучом, с размером пикселя 0,99 мкм, размером FOV примерно 500 × 500 мкм (512 × 512 пикселей) и экспозицией. время 1 с. Стопка z- (толщиной 250 мкм) была захвачена с интервалом 2 мкм. Для измерений того же образца с бесселевым пучком количество пикселей, диапазон сканирования сканирующих зеркал и время экспозиции сохранялись по гауссовой диаграмме, а число усреднения равнялось 4,9.0011
Для измерения активности Ca 2+ в острых срезах регистрировали сигналы флуоресценции системой TPLSM с теми же номерами пикселей и диапазоном сканирования сканирующих зеркал с измерениями просветляющих срезов Sca l eA2, при этом время экспозиции и усреднение число составляло 33 мс и 4 соответственно.
 Спонтанная кальциевая активность промежуточных нейронов SST + была сначала проверена с помощью сканирования гауссовым пучком для проверки состояния здоровья записывающих срезов. Одни и те же области мозга использовались как для гауссовых изображений, так и для изображений, полученных при сканировании пучком Бесселя. Все данные изображений были обработаны и проанализированы с использованием программного обеспечения для обработки изображений (ImageJ и NIS element Ver.4.51, Nikon). Кальциевая активность SST + интернейронов было извлечено из данных замедленной съемки и проанализировано как dF/F 0 . На рис. 4 десять областей интереса (ROI), соответствующих соме интернейронов SST + , были выбраны вручную. F 0 рассчитывали как среднюю яркость пикселя до стимуляции CNO; при расчете среднего значения интенсивности, превышающей два стандартных деления, исключались. Соответствующее изменение флуоресценции, dF/F 0 , оценивали с использованием отношения интенсивности сигнала между каждой временной точкой ( F ) и F 0 .
Спонтанная кальциевая активность промежуточных нейронов SST + была сначала проверена с помощью сканирования гауссовым пучком для проверки состояния здоровья записывающих срезов. Одни и те же области мозга использовались как для гауссовых изображений, так и для изображений, полученных при сканировании пучком Бесселя. Все данные изображений были обработаны и проанализированы с использованием программного обеспечения для обработки изображений (ImageJ и NIS element Ver.4.51, Nikon). Кальциевая активность SST + интернейронов было извлечено из данных замедленной съемки и проанализировано как dF/F 0 . На рис. 4 десять областей интереса (ROI), соответствующих соме интернейронов SST + , были выбраны вручную. F 0 рассчитывали как среднюю яркость пикселя до стимуляции CNO; при расчете среднего значения интенсивности, превышающей два стандартных деления, исключались. Соответствующее изменение флуоресценции, dF/F 0 , оценивали с использованием отношения интенсивности сигнала между каждой временной точкой ( F ) и F 0 .
Чтобы предвидеть изображение, отсканированное лучом Бесселя с использованием устройства создания световой иглы, макрос реконструкции изображения был написан с использованием ImageJ. Макропреобразованное изображение стека z- было измерено с помощью сканирования восстановленного изображения по гауссову лучу, отражающего коэффициент масштабирования в зависимости от расстояния между линзой объектива и целью (рис. 2d).
Ссылки
Conchello, J. A. & Lichtman, J. W. Оптическая секционная микроскопия. Нац. Методы 2 , 920–931 (2005).
КАС Статья Google ученый
Денк В., Стриклер Дж. Х. и Уэбб В. В. Двухфотонная лазерная сканирующая флуоресцентная микроскопия. Science 248 , 73–76 (1990).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
«>
Рабут Г. и Элленберг Дж. Автоматическое трехмерное отслеживание клеток в режиме реального времени с помощью флуоресцентной микроскопии. J. Microsc. 216 , 131–137 (2004).
MathSciNet КАС Статья Google ученый
Отомо, К. и др. Многоточечная сканирующая микроскопия с двухфотонным возбуждением с использованием лазера высокой пиковой мощности с длиной волны 1042 нм. Анал. Sci 31 , 307–313 (2015).
Артикул Google ученый
Отомо, К. и др. Мощный лазерный источник света с длиной волны 918 нм на основе двухфотонной микроскопии с вращающимся диском для зеленых флуорофоров. Биохим. Биофиз. Рез. коммун. 529 , 238–242 (2020).
КАС Статья Google ученый
Лауэр, В.
 Новый подход к оптической дифракционной томографии, позволяющий получить векторное уравнение дифракционной томографии и новый томографический микроскоп. J. Microsc. 205 , 165–176 (2002).
Новый подход к оптической дифракционной томографии, позволяющий получить векторное уравнение дифракционной томографии и новый томографический микроскоп. J. Microsc. 205 , 165–176 (2002).MathSciNet КАС Статья Google ученый
Саймон В. и др. Томографическая дифракционная микроскопия с изотропным разрешением. Optica 4 , 460–463 (2017).
ОБЪЯВЛЕНИЕ Статья Google ученый
Мерц, Дж. Стратегии объемной визуализации с помощью флуоресцентного микроскопа. Оптика 6 , 1261–1268 (2019).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Ботерби Э. Дж., Юшкайтис Р. и Уилсон Т. Сканирующая двухфотонная флуоресцентная микроскопия с увеличенной глубиной резкости. Опц. коммун.
 268 , 253–360 (2006).
268 , 253–360 (2006).ОБЪЯВЛЕНИЕ Статья Google ученый
Терио Г., Конинк Ю. Д. и Маккарти Н. Микроскопия с увеличенной глубиной резкости для быстрой объемной двухфотонной визуализации. Опц. Экспресс 21 , 10095–10104 (2013).
ОБЪЯВЛЕНИЕ Статья Google ученый
Лу, Р. и др. Видеообъемная функциональная визуализация головного мозга с синаптическим разрешением. Нац. Неврологи. 20 , 620–628 (2017).
КАС Статья Google ученый
Кодзава Ю. и Сато С. Световая игольчатая микроскопия с пространственно-перемещенным детектированием для получения объемных изображений с осевым разрешением. науч. Респ. 9 , 11687 (2019).
ОБЪЯВЛЕНИЕ Статья Google ученый
«>Отомо, К. и др. Усовершенствованная микроскопия easySTED, основанная на двухфотонном возбуждении электрическими модуляциями волновых фронтов световых импульсов. Биомед. Опц. Экспресс 9 , 2671–2680 (2018).
КАС Статья Google ученый
Хама, Х. и др. Sca l e: Химический подход к флуоресцентной визуализации и реконструкции прозрачного мозга мыши. Нац. Неврологи. 14 , 1481–1488 (2011).
КАС Статья Google ученый
«>Стернсон С. М. и Рот Б. Л. Хемогенетические инструменты для исследования функций мозга. год. Преподобный Нейроски. 37 , 387–407 (2014).
КАС Статья Google ученый
Тремблей Р., Ли С. и Руди Б. ГАМКергические интернейроны в неокортексе: от клеточных свойств к цепям. Нейрон 91 , 260–292 (2016).
КАС Статья Google ученый
Scheyltjens, I. & Arckens, L. Текущее состояние интернейронов соматостатина в ингибирующем контроле функции мозга и пластичности. Нейропласт. 2016 , 8723623 (2016).

Артикул Google ученый
Сонг, А. и др. Объемная двухфотонная визуализация нейронов с использованием стереоскопии (vTwINS). Нац. Методы 14 , 420–426 (2017).
КАС Статья Google ученый
Хонина С. Н., Казанский Н. Л., Хорин П. А., Бутт М. А. Современные типы аксиконов: новые функции и приложения. 9Датчики 2581 21 , 6690 (2021).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Фэн Г. и др. Визуализация субпопуляций нейронов у трансгенных мышей, экспрессирующих множественные спектральные варианты GFP. Нейрон 28 , 41–51 (2000).
КАС Статья Google ученый
Тинг, Дж. Т., Дайгл, Т.
 Л., Чен, К. и Фенг, Г. Методы острых срезов мозга для взрослых и стареющих животных: применение целевого анализа пэтч-кламп и оптогенетики. Методы. Мол. биол. 1183 , 221–242 (2014).
Л., Чен, К. и Фенг, Г. Методы острых срезов мозга для взрослых и стареющих животных: применение целевого анализа пэтч-кламп и оптогенетики. Методы. Мол. биол. 1183 , 221–242 (2014).Артикул Google ученый
Тинг, Дж. Т. и др. Подготовка острых срезов головного мозга с использованием оптимизированного метода защитного восстановления N-метил-D-глюкамина. Дж. Вис. Эксп. 132 , e53825 (2018 г.).
Google ученый
- 2
- 2
- 2
Даны R и h : r = √2Rh — h 2
где r — радиус основания, R — радиус сферы, h — высота сферического колпачкаEX: Джек действительно хочет победить своего друга Джеймса в игре в гольф, чтобы произвести впечатление на Джилл, и вместо того, чтобы тренироваться, он решает саботировать мяч для гольфа Джеймса.
 Он отрезает идеальный сферический колпачок от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:0011
Он отрезает идеальный сферический колпачок от верхней части мяча для гольфа Джеймса и должен рассчитать объем материала, необходимого для замены сферического колпачка и смещения веса мяча для гольфа Джеймса. Учитывая, что мяч для гольфа Джеймса имеет радиус 1,68 дюйма, а высота сферической крышки, которую срезал Джек, составляет 0,3 дюйма, объем можно рассчитать следующим образом:0011объем = 1/3 × π × 0,3 2 (3 × 1,68 — 0,3) = 0,447 дюйма 3
К сожалению для Джека, Джеймс получил новую партию мячей за день до их игры, и все усилия Джека оказались напрасными.
Коническое усеченное сечение
Коническое усеченное сечение — это часть твердого тела, остающаяся после разрезания конуса двумя параллельными плоскостями. Этот калькулятор вычисляет объем для прямого круглого конуса специально. Типичные усеченные конусы, встречающиеся в повседневной жизни, включают абажуры, ведра и некоторые стаканы. Объем правого конического усеченного конуса рассчитывается по следующему уравнению:
объем = πh(r 2 + rR + R 2 ) где r и R — радиусы оснований, h — высота усеченного конуса
таким образом, чтобы мороженое оставалось упакованным внутри конуса, а поверхность мороженого находилась на одном уровне и была параллельна плоскости отверстия конуса.
 Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:
Она собирается начать есть свой рожок и оставшееся мороженое, когда ее брат хватает ее и откусывает часть нижней части рожка, которая идеально параллельна ранее единственному отверстию. Беа теперь осталась с протекающим мороженым в правом коническом усеченном конусе, и ей нужно рассчитать объем мороженого, который она должна быстро съесть, учитывая высоту усеченного конуса 4 дюйма и радиусы 1,5 дюйма и 0,2 дюйма:объем = 1/3 × π × 4 (0,2 2 + 0,2 × 1,5 + 1,5 2 ) = 10,849 в 3
поверхность, которую можно описать как деформацию сферы за счет масштабирования направленных элементов. Центром эллипсоида называется точка, в которой пересекаются три попарно перпендикулярные оси симметрии, а отрезки, ограничивающие эти оси симметрии, называются главными осями. Если все три имеют разную длину, эллипсоид обычно называют трехосным. Уравнение для расчета объема эллипсоида выглядит следующим образом:
объем = πabc где a , b и c длины осей мясо, поскольку он может поместиться в булочке в форме эллипса.
 Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:
Таким образом, Хабат выдалбливает булочку, чтобы максимально увеличить объем мяса, который он может поместить в свой бутерброд. Учитывая, что осевая длина его булочки составляет 1,5 дюйма, 2 дюйма и 5 дюймов, Хабат вычисляет объем мяса, который он может поместить в каждую выдолбленную булочку, следующим образом:объем = 4/3 × π × 1,5 × 2 × 5 = 62,832 дюйма 3
Квадратная пирамида
Пирамида в геометрии представляет собой трехмерное тело, образованное путем соединения многоугольного основания с точкой, называемой его вершиной, где многоугольник — это фигура на плоскости, ограниченная конечным числом отрезков прямой линии. Существует множество возможных многоугольных оснований для пирамиды, но квадратная пирамида — это пирамида, в которой основание — квадрат. Другое различие, связанное с пирамидами, связано с расположением вершины. Вершина правильной пирамиды находится прямо над центром тяжести ее основания. Независимо от того, где находится вершина пирамиды, если ее высота измеряется как перпендикулярное расстояние от плоскости, содержащей основание, до ее вершины, объем пирамиды можно записать как:
Обобщенный объем пирамиды:
объем = бх где b площадь основания и h высота
Объем квадратной пирамиды:
объем = а 2 ч , где a — длина края основания
ПРИМЕР: Ван очарован древним Египтом и особенно любит все, что связано с пирамидами.
 Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:
Будучи старшим из своих братьев и сестер Ту, Три и Форе, он может легко загнать их в загон и использовать по своему желанию. Воспользовавшись этим, Ван решает воспроизвести древние египетские времена и попросить своих братьев и сестер выступить в роли рабочих, строящих ему пирамиду из грязи с длиной ребра 5 футов и высотой 12 футов, объем которой можно рассчитать с помощью уравнения для квадрата. пирамида:объем = 1/3 × 5 2 × 12 = 100 футов 3
Трубчатая пирамида
Трубка, часто также называемая трубой, представляет собой полый цилиндр, который часто используется для передачи жидкостей или газов. . Вычисление объема трубы по существу использует ту же формулу, что и для цилиндра ( объем = pr 2 h ), за исключением того, что в этом случае используется диаметр, а не радиус, и длина используется, а не высота. Таким образом, формула включает измерение диаметров внутреннего и внешнего цилиндров, как показано на рисунке выше, вычисление каждого из их объемов и вычитание объема внутреннего цилиндра из объема внешнего.
 С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
С учетом использования длины и диаметра, упомянутых выше, формула для расчета объема трубы показана ниже:
55555014объем = π D 1 2 — D 2 2 4 4 4 555555144 555502л , где d 1 — внешний диаметр, d 2 — внутренний диаметр, а l — длина трубы. Ее строительная компания использует только самые экологически чистые материалы. Она также гордится тем, что удовлетворяет потребности клиентов. У одного из ее клиентов есть загородный дом, построенный в лесу, через ручей. Он хочет более легкого доступа к своему дому и просит Беулу построить ему дорогу, обеспечив при этом свободное течение ручья, чтобы не мешать его любимому месту рыбалки.

Танабэ, А. и др. Просвечивающий жидкокристаллический прибор для коррекции первичной комы и астигматизма в биопрепарате в лазерной сканирующей микроскопии с двухфотонным возбуждением. Дж. Биомед. Опц. 21 , 121503 (2016).
ОБЪЯВЛЕНИЕ Статья Google ученый
Танигучи, Х. и др. Ресурс кре-драйверных линий для генетического нацеливания на ГАМКергические нейроны коры головного мозга. Нейрон 71 , 995–1013 (2011).
КАС Статья Google ученый
Скачать ссылки
Калькулятор объема
Ниже приведен список калькуляторов объема для нескольких распространенных форм. Пожалуйста, заполните соответствующие поля и нажмите кнопку «Рассчитать».
Калькулятор объема сферы
Калькулятор объема конуса
Калькулятор кубического объема
Калькулятор объема цилиндра
Калькулятор объема прямоугольного резервуара
|
Калькулятор объема капсулы
Калькулятор объема сферической крышки
Для расчета укажите любые два значения ниже.
|
Калькулятор объема усеченного конуса
|
Калькулятор объема эллипсоида
|
Калькулятор объема квадратной пирамиды
Калькулятор объема пробирки
|
Калькулятор площади поверхности | Калькулятор площади
Объем – это количественная оценка трехмерного пространства, занимаемого веществом. Единицей объема в системе СИ является кубический метр, или 9.0572 м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы. Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Единицей объема в системе СИ является кубический метр, или 9.0572 м 3 . По соглашению объем контейнера обычно представляет собой его вместимость и количество жидкости, которое он может вместить, а не объем пространства, которое вытесняет фактический контейнер. Объемы многих форм можно рассчитать с помощью четко определенных формул. В некоторых случаях более сложные формы можно разбить на более простые совокупные формы, и сумма их объемов используется для определения общего объема. Объемы других, еще более сложных форм, можно рассчитать с помощью интегрального исчисления, если существует формула для границы формы. Помимо этого, формы, которые не могут быть описаны известными уравнениями, могут быть оценены с использованием математических методов, таких как метод конечных элементов. В качестве альтернативы, если плотность вещества известна и однородна, объем можно рассчитать, используя его вес. Этот калькулятор вычисляет объемы для некоторых из наиболее распространенных простых форм.
Сфера
Сфера — это трехмерный аналог двумерного круга. Это идеально круглый геометрический объект, который математически представляет собой набор точек, равноудаленных от заданной точки в его центре, где расстояние между центром и любой точкой на сфере равно радиусу r . Вероятно, наиболее известным сферическим объектом является идеально круглый шар. В математике существует различие между шаром и сферой, где шар представляет собой пространство, ограниченное сферой. Независимо от этого различия, шар и сфера имеют одинаковый радиус, центр и диаметр, и вычисление их объемов одинаково. Как и в случае с окружностью, самый длинный отрезок, соединяющий две точки сферы через ее центр, называется диаметром, д . Уравнение для расчета объема сферы представлено ниже:
| объем = | πr 3 |
EX: Клэр хочет наполнить уксусом идеально сферический воздушный шар радиусом 0,15 фута, чтобы использовать его в битве с водяным шаром против ее заклятого врага Хильды в ближайшие выходные. Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:
Необходимый объем уксуса можно рассчитать по приведенному ниже уравнению:
объем = 4/3 × π × 0,15 3 = 0,141 фута 3
Конус
Конус представляет собой трехмерную форму, которая плавно сужается от своего обычно круглого основания к общей точке, называемой вершиной (или вершиной). Математически конус образован подобно кругу набором отрезков, соединенных с общей центральной точкой, за исключением того, что центральная точка не входит в плоскость, содержащую круг (или какое-либо другое основание). На этой странице рассматривается только случай конечного прямого кругового конуса. Конусы, состоящие из полулиний, некруглых оснований и т. д., которые простираются до бесконечности, рассматриваться не будут. Уравнение для расчета объема конуса выглядит следующим образом:
| объем = | πr 2 ч |
где r — радиус, а h — высота конуса
ПРИМЕР: Беа полна решимости выйти из магазина мороженого с хорошо потраченными 5 долларами, заработанными тяжелым трудом. Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее. Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:
Хотя она предпочитает обычные сахарные рожки, вафельные рожки, бесспорно, крупнее. Она определяет, что на 15 % предпочитает обычные сахарные рожки вафельным рожкам, и ей необходимо определить, превышает ли потенциальный объем вафельного рожка на ≥ 15 % объем сахарного рожка. Объем вафельного рожка с круглым основанием радиусом 1,5 дюйма и высотой 5 дюймов можно рассчитать с помощью приведенного ниже уравнения:
объем = 1/3 × π × 1,5 2 × 5 = 11,781 дюйма 3
Беа также вычисляет объем сахарного рожка и обнаруживает, что разница составляет < 15%, и решает купить сахарный рожок. . Теперь все, что ей нужно сделать, это использовать свою ангельскую детскую привлекательность, чтобы заставить персонал опустошить контейнеры с мороженым в ее рожок.
Куб
Куб является трехмерным аналогом квадрата и представляет собой объект, ограниченный шестью квадратными гранями, три из которых сходятся в каждой из его вершин и все перпендикулярны соответствующим смежным граням. Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр. Ниже приведено уравнение для расчета объема куба:
Куб является частным случаем многих классификаций фигур в геометрии, включая квадратный параллелепипед, равносторонний кубоид и правильный ромбоэдр. Ниже приведено уравнение для расчета объема куба:
объем = 3
где a — длина ребра куба
ПРИМЕР: Боб, родившийся в Вайоминге (и никогда не покидавший штат), недавно посетил родину своих предков в Небраске. Потрясенный великолепием Небраски и окружающей средой, непохожей ни на что другое, с чем он когда-либо сталкивался ранее, Боб понял, что ему нужно привезти часть Небраски домой с собой. У Боба есть кубический чемодан с длиной ребра 2 фута, и он вычисляет объем почвы, который он может унести с собой домой, следующим образом:
объем = 2 3 = 8 футов 3
Цилиндр
Цилиндр в его простейшей форме определяется как поверхность, образованная точками на фиксированном расстоянии от заданной прямой оси. Однако в обычном употреблении «цилиндр» относится к прямолинейному круговому цилиндру, основаниями которого являются окружности, соединенные через их центры осью, перпендикулярной плоскостям его оснований, с заданной высотой h и радиусом r . . Уравнение для расчета объема цилиндра показано ниже:
. Уравнение для расчета объема цилиндра показано ниже:
объем = πr 2 ч
где r — радиус, а h — высота резервуара
ПРИМЕР: Кэлум хочет построить замок из песка в гостиной своего дома. Поскольку он решительно выступает за переработку отходов, он нашел три цилиндрические бочки с незаконной свалки и очистил их от химических отходов, используя средство для мытья посуды и воду. Каждая бочка имеет радиус 3 фута и высоту 4 фута, и Кэлум определяет объем песка, который может вместить каждая, используя приведенное ниже уравнение:
объем = π × 3 2 × 4 = 113,097 фута 3
Он успешно строит замок из песка в своем доме и, в качестве дополнительного бонуса, ему удается экономить электроэнергию на ночном освещении, так как его замок из песка светится ярко-зеленым в темноте. темнота.
Прямоугольный резервуар
Прямоугольный резервуар представляет собой обобщенную форму куба, стороны которого могут иметь различную длину. Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
Он ограничен шестью гранями, три из которых сходятся в его вершинах и все перпендикулярны соответствующим смежным граням. Уравнение для расчета объема прямоугольника показано ниже:
объем= длина × ширина × высота
ПРИМЕР: Дарби любит торт. Она ходит в спортзал по 4 часа в день, каждый день, чтобы компенсировать свою любовь к тортам. Она планирует пройти по тропе Калалау на Кауаи, и, хотя Дарби в отличной форме, она беспокоится о своей способности пройти тропу из-за отсутствия торта. Она решает упаковать только самое необходимое и хочет наполнить свой идеально прямоугольный пакет длиной, шириной и высотой 4 фута, 3 фута и 2 фута соответственно тортом. Точный объем торта, который она может поместить в свою упаковку, рассчитывается ниже:
объем = 2 × 3 × 4 = 24 фута 3
Капсула
Капсула представляет собой трехмерную геометрическую форму, состоящую из цилиндра и двух полусферических концов, где полусфера представляет собой половину сферы. Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
Отсюда следует, что объем капсулы можно рассчитать, комбинируя уравнения объема для сферы и прямого кругового цилиндра:
| объем = πr 2 ч + | πr 3 = πr 2 ( | р + ч) |
где r радиус и h высота цилиндрической части
Джо может взять с собой капсулу времени, которую он хочет похоронить для будущих поколений в своем путешествии самопознания через Гималаи:
объем = π × 1,5 2 × 3 + 4/3 × π ×1,5 3 = 35,343 футов 3
Сферическая крышка
Сферическая крышка представляет собой часть сферы, отделенную от остальной части сферы плоскостью. Если плоскость проходит через центр сферы, сферическая шапка называется полусферой. Существуют и другие различия, в том числе сферический сегмент, где сфера разделена на две параллельные плоскости и два разных радиуса, где плоскости проходят через сферу. Уравнение для расчета объема сферической шапки получено из уравнения для сферического сегмента, где второй радиус равен 0. Относительно сферической шапки, показанной в калькуляторе:
Уравнение для расчета объема сферической шапки получено из уравнения для сферического сегмента, где второй радиус равен 0. Относительно сферической шапки, показанной в калькуляторе:
| объем = | πh 2 (3R — h) |
Имея два значения, предоставленный калькулятор вычисляет третье значение и объем. Уравнения для преобразования между высотой и радиусом показаны ниже:
Данный R и R : H = R ± √r 2 — R 2
| .0014 | ч 2 + г 2 |
| 2ч |
