Как сделать красивую цифру на день рождения: Объемные цифры на День Рождения: схемы, уроки

Содержание

Создаем объемную цифру 4 на день рождения — Сделай сам — 22 июля — 43474634663

Хочу рассказать вам, как можно своими руками сделать цифру 4 на день рождения ребенку.

Для этого не нужно владеть специальными навыками и умениями, необходимо только желание, отличное настроение, необходимые материалы и 18-20 часов свободного времени 🙂

Для изготовления цифры нам понадобятся:

картон;
карандаш;
линейка;
малярный скотч;
горячий клей;
ножницы;
канцелярский нож;
небольшая веревочка;
деревянные брусочки;
3 рулона гофрированной бумаги (у меня итальянская, плотностью 180 г, 558 тон).

Для начала изготовим каркас нашей циферки 🙂 На фото ниже указаны все размеры. У меня это шаблон на самом обычном картоне. Саму же цифру я делаю из трехслойного картона высокого качества (так как сдаю их в аренду и нужно, чтобы они прослужили как можно дольше). Но и обычная картонная коробка подойдет 🙂

Вырезаем 2 таких заготовки (лицевую и изнаночную стороны) и боковинки толщиной 10 см.

Перед тем, как начать собирать каркас цифры, на 1 заготовке из заготовок делаем отверстия шилом или маленькой отверточкой и протягиваем небольшую веревочку, которая потом будет служить ручкой! С ручкой очень удобно. Можно свободно переносить готовую цифру, не сминая фунтики. А еще во время фотосессии ее можно повесить на стену 🙂

Собираем каркас с помощью малярного скотча. Стыки изнутри обязательно нужно промазать горячим клеем!

Затем приклеиваем брусочки, утяжеляем хвостик и спинку нашей четверки. В этом плане цифра 4 является самой сложной в изготовлении, так как необходимо, чтобы она устойчиво стояла на одной ножке и не заваливалась на нос. Для утяжеления можете также использовать рейки или марлбсы, а может вы придумаете что-то еще 🙂

Не во всех мастер-классах пишут про горячий клей, многие ограничиваются малярным скотчем. Однако настоятельно советую со всех сторон, во все щели залить клей, придавить все стыки — держаться будет намертво 🙂

Основание будем приклеивать в самый последний момент, когда цифра будет почти полностью задекорирована.

Это вид с изнанки. Без основания нос все равно заваливается.

Далее я буду декорировать стыки. Для этого вырезаем полоску бумаги толщиной 2 см и хорошенько растягиваем ее.

Приклеиваем на горячий клей 🙂

Так же необходимо проклеить бумагой внутреннюю часть цифры. И вот что у нас получилось 🙂

Когда каркас готов — начинаем готовить фунтики. Берем бумагу, нарезаем ее на полоски шириной 5 см. Хорошень растягиваем их и нарезаем на квадратики 5 х 5 см.

Клеить будем в технике торцевание. Наверняка все уже знают, что и как. Но на всякий случай покажу 🙂
Берем карандаш и оборачиваем вокруг него нашу квадратик, вот так.

Получается фунтик 🙂 Наносим на кончик каплю горячего клея и приклеиваем его к цифре.

Почти всю цифру мы обклеиваем фунтиками 5 х 5 см. А низ и левую нижнюю боковинку фунтиками 4 х 4 см.

Когда цифра будет почти готов, приклеим основание на горячий клей! На фото видно, как я его утяжелила.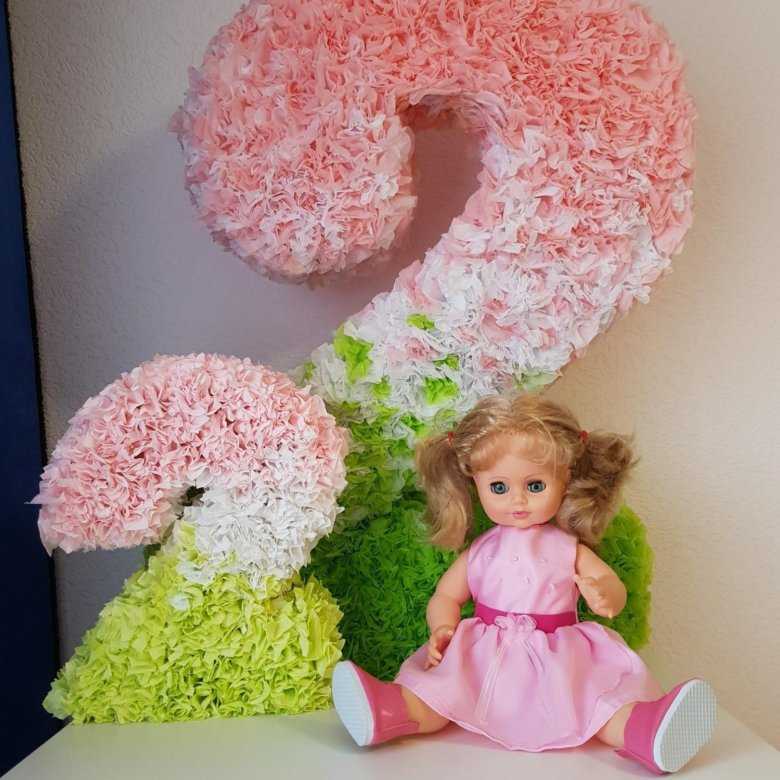

Доклеиваем ножку цифры фунтиками. И декорируем заднюю сторону цифры. Я просто обклеила бумагой.

И еще такой момент, 2 марблса тут не случайно. Готовая цифра продолжала предательски заваливаться на нос. Вывод такой — необходимо лучше утяжелять спинку и брать более тяжелый бруски/рейки. По 4 практически нет мастер-классов, поэтому пришлось делать ее методом проб и ошибок. Так вот, эти два камешка здорово меня выручили 🙂 Приклеила их на горячий клей и вуаля, цифра приняла устойчивое вертикальное положение.

Надеюсь, что мой мастер-класс окажется вам полезным. Пробуйте, экспериментируйте и все у вас получится!

Источник

Понравилась статья? Подпишитесь на канал, чтобы быть в курсе самых интересных материалов

Цифры на день рождения своими руками

Чаще все мы можем наблюдать на праздниках цифры из маленьких шаров. Особенно на первые дни рождения родители обычно заказывать цифру соответствующую возрасту ребенка. А на самом деле сделать такую цифру на день рождения своими руками красивее и необычнее можно из любого другого материала. Даже если делать цифру надо срочно – у вас, наверняка, найдется картон и бумага, а у рукодельниц ткань или нитки. А уж если заранее готовиться, то можно подготовить к оформлению распечатанные фотографии или что-то совсем необычное.

БУМАГА

Итак, берем бумагу и картон. Вырезаем из картона цифру нужного нам размера шириной примерно 5 см. Берем папирусную бумагу или просто тонкую цветную и начинаем творить. Делаем цветы. Для этого берем 6 листов бумаги, соединяем вместе, всю пачку складываем гармошкой. Затем делим гармошку на три части (примерно по 12 см), посередине перевязываем, концы округляем, разделяем слои и начинаем выворачивать лепестки.

Когда наберется достаточно цветов, приклеиваем их к нашему картону. Получается такая красота.

Еще бумажные цветы можно пришивать. Только уже за основу возьмем не картон, а ткань, которой обтянем нужного размера рамку. В таком случае цифра будет ярче, если цвета подберем контрастные сочетания ткани и бумаги.

А для изготовления цветов возьмем несколько слоев бумаги, вырежем их нее квадраты и сложим все пополам, потом еще раз пополам, потом как кусок пирога. Берем ножницы и вырезаем полукруг. У нас с легкостью получится нужные нам цветы. Количество цветов зависит от возможностей ножниц.

Берем получившиеся цветы, соединяем несколько цветочков и пришиваем их к нашей ткани, по нарисованной широкой цифре на полотне. Будет красивее если цифра будет шириной в два-три цветка.

Еще, чтобы сделать цифру на день рождения своими руками, можно начать с бумажных цветов. Берем бумагу нужного цвета и вырезаем круг. Рисуем на круге спираль или можно сразу резать бумагу по спирали. Затем соединяем (закручиваем) получившиеся полоски спирали в цветок и приклеиваем на картон. Цветы при этом будут ярче смотреться, если будут разного размера и цвета.

Самый простой вариант: просто нарезать гофрированную бумагу на полоски чуть длиннее, чем ширина цифры и приклеить на картонную цифру. Получается платье в оборочках. Для девочек очень нежный вариант.

Ткани и ленты

А уж если у вас есть много ленточек, смело режьте из на небольшие кусочки примерно по 20 см. (зависит от величины цифры). Первый вариант – если у вас широкие ленточки – делаем красивые бантики. Они словно бабочки сядут на вашу цифру.

А второй вариант, если у вас в наличии узкие ленточки. Тогда долго не думаем, в просто завязываем узелки и смело приклеиваем их на цифру. Разноцветные ленточки сделают цифру более яркой и веселой, а однотонные – спокойной и торжественной.

Очень красиво смотрятся в качестве цифры атласные цветы. Их совсем не сложно сделать. Вырезаем из атласной ткани или широкой атласной ленты три круга: побольше, средний и маленький. Немного обугливаем края свечкой и соединяем лепестки иголкой.

Чаще всего для цифры на день рождения своими руками мы испольщуем картон, но в данном случае хорошо за основу цифры взять пенопласт. И тогда можно смело втыкать наши цветы так, чтобы основы не было видно.

НИТКИ

Для красивой цифры можно использовать нитки. Берем снова картонную цифры или делаем ее объемной. Для этого нужно побольше картона и скотч. Соединяем части цифры скотчем

Берем нитки и приклеиваем их в торце. Остальную. поверхность обвязываем нитками одного цвета или разных цветов.

Можно не готовить объемную цифру, а обмотать плоский картон. Получиться ничуть не хуже. Цветовую гамму только стоит подобрать под стиль вашего праздника.

Еще нитками можно сплести цифры, обвязывая гвоздики. В дощечку вставляем кнопки или гвоздики по периметру цифры и начинаем делать паутинку.

ФОТОГРАФИИ

Очень интересны вариант цифры на день рождения своими руками получаются из фотографий. Можно в фотошопе сразу собрать коллаж в форме цифры и распечатать. Можно скрепить две бумаги, на одной наклеить фотографии, на другой вырезать широкую цифру. Или просто сложить из фотографий цифры и прикрепить к стене.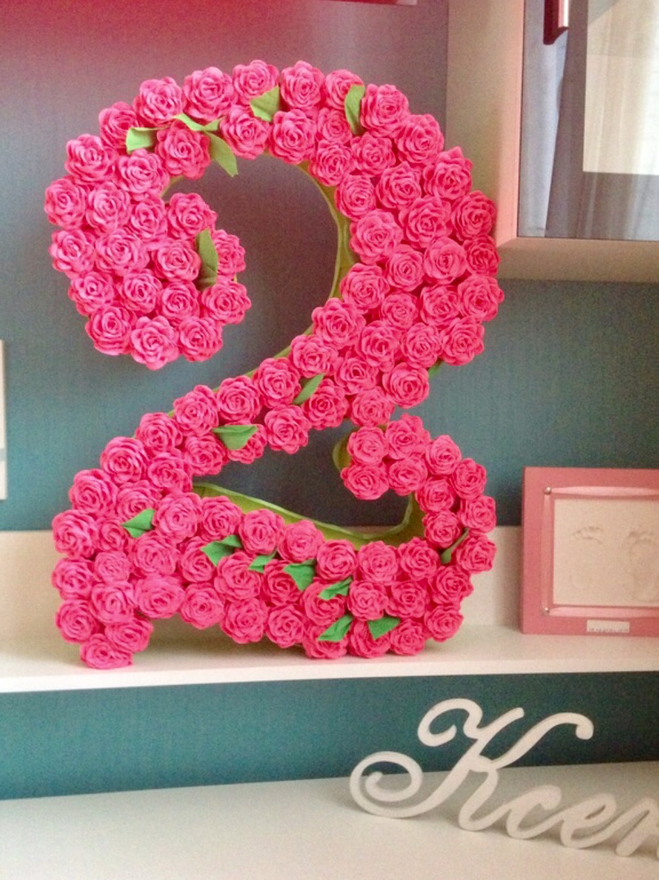

ИЗ РАЗНООБРАЗНЫХ МАТЕРИАЛОВ

А если у вас ребенок чем-то увлекается или у вас есть интересный материал, используйте его для изготовления цифры своими руками. Например, возьмите лего или мозаику, или воздушные шарики. Посмотрите вокруг – у вас точно что-то есть полезного для цифры: скрепки, пуговицы, прищепки, игрушки и многие другие вещицы. Праздник – день рождения для того и создается, чтобы фантазировать и творить.

Источник

Как сделать потрясающий торт с цифрами для вашей следующей вечеринки

Огромной тенденцией в тортах в этом году стали великолепные торты с буквами и цифрами , которые вы, вероятно, рассматривали в Instagram! Вы знаете гигантские номера с несколькими слоями печенья и глазурью, покрытыми всевозможными сладостями, от макарон до безе, от конфет до цветов, от рожков мороженого до печенья? Да, я говорю о красотках! Присоединяйтесь ко мне, когда я загляну за кулисы, чтобы увидеть, как создаются эти прекрасные творения, и черпать вдохновение для вашего следующего посещения кухни!

Этот модный дизайнерский торт начал появляться в пекарнях повсюду в 2018 году и до сих пор пользуется популярностью! Может быть, как и я, вы задавались вопросом, это торт, печенье, пирог? Оказывается, это зависит от того, кто это делает! И торты имеют форму не только цифр… Буквы и символы также очень популярны.

В конечном счете, числовые торты — это многослойные деликатесы, увенчанные цветами, конфетами, печеньем и другими вкусностями, чтобы соответствовать праздничному событию. Давайте посмотрим на несколько красивых примеров, которые мы нашли, включая рецепты и видеоуроки, чтобы вы могли воссоздать собственный шедевр дома!

Во-первых, давайте начнем с пирога с номером. Александра в Everyday Delicious делится своим восхитительно выглядящим рецептом торта с лимонным кремом и малиной, который она превратила в торт номер один на день рождения своей дочери. Простая малина, безе и свежие цветы выглядят просто великолепно!

Что мне больше всего нравится в этой тенденции, так это то, как пекари персонализируют начинку для тортов с цифрами в соответствии с темой вечеринки или интересами и пристрастиями именинника. Возьми это Торт номер два , например… его основные цвета идеально подходят для маленьких детей, которым не понравятся игривые рожки мороженого сверху! На самом деле, это был бы идеальный торт для вечеринки у бассейна в честь двухлетнего дня рождения, которую мы недавно представили!

instagram.com/p/ByEOl3-nfu9/?utm_source=ig_embed&utm_campaign=loading» data-instgrm-version=»13″>
Посмотреть этот пост в Instagram
Пост, которым поделился пользователь ?????????????????????? ???????????????????????? (@jello_sweets)
Если вы визуал и хотите увидеть закулисный урок о том, как создаются эти необычные торты, посмотрите это видео от @anniscakery_. Ее Торт номер 30 состоит из торта, покрытого джемом (ням!) и глазурью. Я люблю свежие цветы на торте, и эти розы прекрасно смотрятся рядом со свежими фруктами и макаронами!

Посмотреть этот пост в Instagram
Пост, которым поделилась Аннам (@anniscakery_)
Валентина по адресу Фея Пекарни поделилась своим рецептом безглютенового торта с шоколадными конфетами для вечеринки по случаю 13-го дня рождения! Ее торт также был полностью тортом (а не сложенным в стопку печеньем или пирогом), и у нее есть несколько отличных советов по созданию идеальных фигур с числами. Мне нравится тема шоколадного печенья и конфет, а вам?!
Вы даже можете добавить имя именинника на верхнюю часть торта, как это сделала @sweet.events.by.sandra на этом торте номер 9 ! Посмотрите на все детали здесь… балетки и танцовщица, желейные бобы, зефир, крендельки в шоколаде, шоколадные конфеты, карамельные жемчужины… о, боже мой!!

Посмотреть этот пост в Instagram
Пост, которым поделился ♡???????????????????????????♡ #?????????????????? ?? (@sweet.events.by.sandra)
И, конечно же, вам не нужно делать номер… торты с буквами также очень популярны! Назовите по буквам имя именинника, сделайте монограмму невесты или как насчет первого инициала ребенка, которого вы приветствуете! Вот взгляните на учебник Letter R Cake … на самом деле он не выглядит таким уж сложным, не так ли?
instagram.com/p/Bxa5lM7DK5x/?utm_source=ig_embed&utm_campaign=loading» data-instgrm-version=»13″>
Посмотреть этот пост в Instagram
Публикация Bru Cake Boutique (@brucakeboutique)
Теперь, когда вы полны вдохновения и идей, какую букву и цифру вы собираетесь испечь дальше?! Оставьте комментарий и дайте мне знать, и обязательно закрепите этот пост на следующей вечеринке!
13 удивительных чисел вокруг нас — когда красота встречается с математикой | Софиен Каабар, CFA
www.pxfuel.com
Иногда числа находятся с помощью красивых уравнений и формул. Они также могут иметь математическую красоту, поскольку их свойства предлагают предсказуемый результат, привлекательный визуально и интеллектуально. От бесконечности до золотого сечения, ниже мы обсудим 13 удивительных чисел в природе.
Aleph Null — красивая концепция. Это наименьшее бесконечное число. Я знаю, о чем вы думаете, бесконечность должна быть всего лишь одним понятием, а не множеством бесконечных чисел. Ведь если есть бесконечность больше другой бесконечности, то первая определенно не бесконечность .
Предположим, что у нас есть базовое представление о том, что такое бесконечность (обсуждается ниже, 12 в списке). Алеф нуль — это количество натуральных чисел (0, 1, 2, 3 и т.д.). Это понятие или число огромно по размеру и бесконечно.

Что, если мы посчитаем все натуральные числа два или три раза? После завершения первого набора у нас будут числа, выходящие за пределы натуральных чисел в 9.0003 заказ . Итак, нам понадобится порядок чисел, иначе известный как порядковый номер. Следующим числом после Алеф Нуль является омега (‎ω), затем следует ω + 1. Эти два последних числа являются не количественными числами, а порядковыми числами, то есть они представляют свое положение относительно горизонтальной оси . Приведенный ниже график является упрощенным представлением. Каждый набор может представлять существующий набор натуральных чисел, и каждый набор имеет мощность ℵ0. Добавление одного после первого набора не меняет кардинальность (вы можете просто изменить порядок, и вы все равно останетесь с кардинальностью Алеф Нуль).

Полезно думать о них как о ординалах (порядке). Следовательно, первое порядковое трансфинитное число после набора — это то, что мы обсуждали выше. «ω»

Представление спички. Источник изображения: Википедия.

У вас нет омега-яблок, но вы можете финишировать омега в гонке (если вы действительно плохи)

Интересно, что ω + 1 не обязательно больше, чем ω, оно просто идет после него. Это все слишком много, чтобы принять во внимание, поэтому рассмотрение вещей в перспективе должно помочь. Вот что мы должны знать:

Бесконечность и Алеф Нуль — две разные вещи. Первое — это просто крайняя предельная идея, лежащая на числовой оси, а второе — просто размер множества (мощность).
Количество элементов — это размер набора, а количественные числительные представляют количество (1, 2, 459, 1002 и т. д.), тогда как порядковый номер — это порядок набора, а порядковые числа представляют порядок (1-й, 2-й, 66-й и т. ).
Так же, как есть бесконечные кардиналы, существуют и бесконечные ординалы, и первое бесконечное (неисчисляемое) порядковое число — это то, что мы обсуждали выше, омега ω.
Следуя этой логике, Алеф один является мощностью омеги ω.

Алеф Нуль — это только первый из огромного набора других «Алефов». Vsauce сделал потрясающее видео, в котором обсуждается эта концепция, и я очень рекомендую его.

Итак, это скорее идея или концепция , чем число. Символ часто называют лемнискатой ∞ . Прежде чем обсуждать характеристики и забавные факты о бесконечности, важно отметить, что число пи (обсуждаемое ниже по списку) считается формой бесконечности. Разумеется, под этим мы подразумеваем диапазон чисел после точки 3,14159.… Вот почему бесконечность — это концепция, а не то, что мы можем измерить количественно. Другой пример исходит из прекрасного поля фракталов. Возьмем, к примеру, простую снежинку Коха, которую можно разделить на бесконечно малые снежинки одинаковой формы.

https://tenor.com/view/koch-fractal-koch-curve-koch-snowflake-infinite-gif-13239066

Интересно, что когда мы думаем о бесконечности, мы представляем себе постоянно растущую меру, но она не расширяется или становится больше. Это уже то, что есть.

Давайте обсудим две простые темы, связанные с бесконечностью (те, которые не требуют какой-либо мозговой активности, потому что на данном этапе мне нужно вздремнуть после разговоров об Алеф Нуль и Бесконечности). Интересно, Георг Кантор отец теории множеств и исследований бесконечности был институционализирован во многие моменты своей жизни):

Естественно, 0,99999 имеет девятки, стремящиеся к бесконечности, так что приблизительно мы знаем точно, что оно равно 1 . Доказывая его алгебраически также возможно:

Если у нас есть x = 0,9999 , то

10x = 9,9999

, если мы вычитаем x с каждой стороны, у нас будет

9x = 9999 -0,999999999

. 0005

9X = 9

Деление на 9

X = 1

Странно, да?

Любое число, вычтенное из самого себя, даст ноль. Но бесконечность — это не число. Следовательно, давайте попробуем проверить:

∞ — ∞ = 0

∞ — ∞ + 1= 0 + 1 # Добавляем 1 к обеим сторонам

+ 1 — ∞ Зная, что = 1 # = ∞, мы можем упростить уравнение

Мы получили совершенно другой результат. С помощью этого метода мы можем получить бесконечность минус бесконечность, чтобы получить любое число, которое мы хотим. Таким образом, ответ на ∞ — ∞ не определено.

Наконец, нас также учат, что мы не можем делить на 0. Нас учат, что 1 / 0 = Undefined, однако это не ложно, но не раскрывает всей истории. Подумайте об этом интуитивно, если вы разделите 1 яблоко на 0 человек, сколько человек вам понадобится, чтобы покрыть все яблоко? Естественно, это форма бесконечности, которая никогда не схлопывается .

Итак, изначально 1/0 = ∞ . Почему нас учат, что результат не определен? Просто, когда у нас есть 1/маленькие положительные числа, стремящиеся к нулю, просто предположить, что 1/0 = ∞ . Дело в том, что здесь бесконечность — это положительная бесконечность. А если мы делаем 1/маленькими отрицательными числами, стремящимися к нулю, то можно также считать, что 1/0 = — ∞ . Итак, что это? 1/0 = ∞ или 1/0 = — ∞ ? Что ж, ответ undefined .

Итоговая таблица операций на бесконечности:

∞ + ∞ = ∞
-∞ + -∞ = -∞
∞ × ∞ = ∞
-∞ × -∞ = ∞
-∞ 0 × ∞4

Буква i обозначает мнимое число. Определение мнимого числа состоит в том, что когда мы возводим его в квадрат, это дает нам отрицательный результат. Это не то, о чем мы обычно думаем, возводя числа в квадрат, потому что мы знаем, что умножение двух одинаковых символов всегда даст положительный результат. Но это не мешает нам создать аксиому, запрещающую существование таких чисел. Мы называем их воображаемыми, потому что они не должны существовать. Чему равен квадратный корень из -6? Мы не знаем. Калькулятор выдаст вам недопустимую ошибку ввода, потому что какие два числа нужно перемножить, чтобы получить отрицательное число? Но прелесть математики в том, что, в отличие от других научных инструментов, вы можете предположить, что вещи существуют, и настроить их так, чтобы они существовали, если они вам не подходят.

Концепция мнимых чисел проста. Мы можем предположить (или вообразить), что они существуют. Чем они полезны? Ну, мы можем решать уравнения, которым нужен квадратный корень из отрицательного числа. Вот пример:

Что такое √4 ? Просто, это 2.
Что такое √-4? Немного сложнее, но ответ 2i.

Мы добавляем i для представления мнимого числа, чтобы 2, возведенное в степень 2, равнялось -4. Давайте проверим очень простое уравнение, которое обычно не имеет решения, и посмотрим, как оно решается с помощью мнимых чисел:

Очевидно, что x, возведенный в степень 2, никогда не может дать отрицательное число (-1 в нашем случае), поэтому мы просто предполагаем, что ответ (как мы сделали выше) умножается на i.

Вы можете представить себе квадратный корень из -1 (√-1) как исходное мнимое число. Как и в числе 1 для действительных чисел. Другое использование мнимых чисел заключается в их объединении с натуральными числами для получения комплексных чисел (например, 7i + 12) и в электричестве с помощью соответствующих токов.

Гугол равен 10, за которым следуют 100 нулей, поэтому, чтобы представить ситуацию в перспективе, подумайте о следующем числе: 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 ,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, 000, или вы можете просто быть нормальным и думать об этом так:

Это примерно 70! (Факториал). что составляет 70 х 69 х 68 х 67 х 66 х 65 х 64 х 63 х 62 х 61 х 60 х 59 …. x 1

Чтобы еще больше усложнить наши мысли, существует число под названием Googol plex, которое равно 10 в степени Googol и записывается как:

Интересно отметить, что компания Google — это неправильное написание названия Googol. Это действительно умный способ назвать вашу поисковую систему. Это число в основном используется в астрономических исследованиях, таких как большое замораживание Вселенной.

Это мое любимое число, и, вероятно, оно предназначено для торговли, но я также нахожу его визуально и математически красивым. В геометрии мы склонны находить его скрытым во многих местах, например:

Окружность. Он имеет 360 градусов (3 + 6 + 0 = 9).0003 9 )
Разрезанный пополам круг. Каждая половина равна 180 градусам (1 + 8 + 0 = 9 )
Круг, разрезанный на четыре части. Каждая четверть равна 90 градусам (9 + 0 = 9 )
Круг разрезан на 8 частей. Каждая часть равна 45 градусам (4 + 5 + 0 = 9 )
Круг разрезан на 16 частей. Каждая часть равна 22,5 градуса (2 + 2 + 5 = 9 )
Круг разрезан на 32 части. Каждая часть равна 11,25 градуса (1 + 1 + 2 + 5 = 9 )
Правильный многоугольник внутри круга. Каждый угол равен 60 x 3 (180 = 1 + 8 = 9 )
Квадрат. Каждый угол равен 90 x 4 (360 = 3 + 6 + 0 = 9 )

Следующие фигуры и их углы.

Источник: wikipedia.org
Слева направо: Пентагон, Восьмиугольник, Декагон.
Пятиугольник = 108 = 1 + 0 + 8 = 9 // 72 = 7 + 2 = 9
Восьмиугольник = 135 = 1 + 3 + 5 = 9 // 45 = 4 + 5 9
Десятиугольник = 144 = 1 + 4 + 4 = 9 // 36 = 3 + 6 = 9
Кроме того, если мы добавим цифры, которые стоят перед числом 9 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36). Тогда у нас будет, как обычно, 3 + 6 = 9
Умножение цифр, стоящих перед 9 , и суммирование их элементов всегда даст нам 9 , примеры:
9 x 1 =
3 4
3 9 010008
9 х 3 = 27 = 2 + 7 = 9
9 x 7 = 63 = 6 + 3 = 9
9 x 9 = 81 = 8 + 1 = 9
, примеры:
1 / 9 = 0,11111
3 / 9 = 0,33333
7 / 9 = 0,77777
Если вы фанат большой теории BANG, тогда вы должны Я слышал, как доктор Шелдон Купер говорил, почему 73 — идеальное число, вот цитата:
“ Лучшее число 73.
Почему? 73 — 21-е простое число. Его зеркало 37 является 12-м, а его зеркало 21 является произведением 7 и 3 . ”’”
“ В двоичном коде 73 является палиндромом, 1001001, который в обратном порядке равен 1001001 . »’
Цитаты взяты из сериала из 10 серии 4 сезона, которая по совпадению является 73 -й серией шоу (и годом рождения Джима Парсонса, актера, изображающего Шелдона).
Назван в честь Леонарда Эйлера, e — иррациональное число и основание натуральных логарифмов. Интересно, что число Эйлера известно с точностью до 1 триллиона знаков [источник: mathisfun.com]. Оно находится по следующей формуле:
Когда n приближается к бесконечности, мы получаем более четкое представление о значении e . Когда n = 100 000, e = 2,71827. Интересное свойство

e состоит в том, что его 9Наклон 0003 равен его значению .

Он также используется в финансах для расчета сложных процентов. Я полагаю, что те из вас, кто уже прошел тест CFA, знакомы с этой информацией.

Леонардо Боначчи, также известный как Леонардо Фибоначчи (это прозвище означает «сын Боначчи»), создал одну из самых захватывающих серий в нашей вселенной, используя простые методы сложения и наблюдая за популяциями кроликов. Теперь, чтобы быть справедливым, есть некоторые свидетельства того, что индийские математики знали эту последовательность заранее, мы будем придерживаться общепризнанного факта, что Фибоначчи придумал эту последовательность (хотя, зная яркую научную и математическую историю индийских исследователей, я бы не удивлюсь, узнав, что они были первыми, кто обнаружил это).

Числа Фибоначчи получаются с помощью следующей простой формулы для n >

Это дает нам следующую последовательность, уходящую в бесконечность:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ….

Прелесть этой последовательности в том, что она связана с природой. Например, появляется цветение артишока, лепестки некоторых цветов, таких как ромашки, медоносные пчелы и т. д. Встречается ли это даже в спиралях галактики?

Существует даже очень интересное наблюдение, основанное на фактах, которое предполагает, что размеры Земли и Луны находятся в соотношении Фи, образуя Треугольник, основанный на 1,618, Гэри Мейснера. Но что такое Phi и что это за 1,618?

Если мы возьмем любые два последовательных числа в последовательности, их отношение (Xn / Xn-1) приблизится к 1,618, что мы называем золотым сечением:
3 / 2 = 1

.5
13 / 8 = 1,6 66
55 /34 = 1,61 764
233 /144 = 1,6180 5
…
317,811 / 196,418 = 1,6180 3

Going To Infinity, Gatios Gets Gets gatios gatios getios getios getios getios getios getios getios gatios getios gatios gatios gatios letios letios gatios gatios gatios gatios gatios gatios gatios gatios gatios gatios до 3

. известный как Фи (ϕ). Мы обсудим Фи более подробно ниже по списку.

Спираль Фибоначчи.

Многие из нас видели фильм «Число 23 », в котором Джим Керри изображает Уолтера Воробья как человека, который становится одержимым числом 23 , прочитав об этом в книге. Считается, что это число таинственным образом совпадает со многими событиями по всему миру и , хотя это может быть прекрасным примером

Апофения , , все же интересно перечислить некоторые события, которые имеют 23 9В них встроено число 0004:
Трагические события 11 сентября могут составить 23 , если мы запишем полную дату следующим образом: 9 + 11 + 2 + 0 + 0 + 1 = 23 . Конечно, мы могли бы также сделать 9 + 11 + 2001 = 2021.
Согласно парадоксу дня рождения, 23 — это наименьшее количество случайно выбранных людей, необходимое для получения по крайней мере 50%-го шанса иметь по крайней мере двух человек. с таким же днем рождения. Для любопытства, 70 человек дают нам 99,99.% шанс.
Уильям Шекспир родился 23 апреля, по совпадению, он умер 23 апреля, а также. конечно, дата рождения точно не известна (Крещен 26-го), но широко распространено мнение, что это 23 апреля.
Титаник затонул 15 апреля 1912 года. Суммируя полную дату (включая число апреля), мы получаем 4 + 1 + 5 + 1 + 9 + 1 + 2 = 23 . Конечно, это начинает напоминать отслеживание данных и поиск шаблонов, потому что мы выбираем даты для суммирования и те, которые не суммируем.
Земля наклонена в плоскости своей орбиты на 23 ,5 градуса. Мы можем рассматривать 5 как 2 + 3, просто чтобы было интереснее. Конечно, ось вращения Земли наклонена на 66,5 градусов по отношению к плоскости ее орбиты, но это не очень здорово знать.
Сообщение Аресибо состоит из 1679 битов, расположенных в 73 строках по по 23 символов в строке. Это, конечно, придумано людьми, но все равно интересно. Сообщение Аресибо — это сообщение, отправленное с Земли в космос в поисках разумной жизни. Подводит итог нашей жизни.
У человека 23 пары хромосом.
Сумма первых 23 простых чисел равна 874, что делится на 23 . Спасибо, Википедия.
Бомба на Хиросиму была сброшена в 8:15. 8 + 15 = Трагическое событие, унесшее тысячи жизней. Кроме того, 8 + 15 = 23 .
23 — наименьшее простое число, состоящее из последовательных цифр
Тамплиеры имели 23 Великих Магистров.
В среднем кровь человека циркулирует по всему телу каждые 23 секунды.
И, наконец, порядковый номер 23 в этом списке равен 5, что снова составляет 2 + 3, но это было выдумано. Суть в том, что хотя числа и красивы, не все они содержат какие-то загадочные элементы. Я думаю, что число 23 немного преувеличено, учитывая имеющиеся у нас доказательства. В этом списке есть много других чисел с гораздо более интересными характеристиками.
Знаменитое иррациональное число, представляющее отношение длины окружности к ее радиусу. Кто из нас не встречал этот номер?
Если мы нарисуем круг диаметром 1, то длина окружности будет равна 3,14159 … что просто обозначается буквой π . Это просто окружность на диаметр. Теперь нам не нужно возвращаться к понятиям геометрии средней школы, поэтому я просто перечислю два интересных свойства числа π :
Его цифры продолжаются до бесконечности без какой-либо закономерности.
Мы все знаем приближение 22/7 для Pie. Но никакое соотношение не может дать точную стоимость пирога, потому что это иррациональное число 9.0014 .
Почему я включил Тау? Некоторые математики спорят о полезности π и вместо этого предлагают Тау, который равен просто τ = 2π . Многие математики утверждают, что Тау больше подходит для вычисления окружностей. Их интуиция верна, когда мы хотим углубиться в детали, но кто не любит Pi(e) ?
Интересно отметить, что существует день числа Пи, который отмечается каждый год 14 марта (дата в США отображается в формате ММ/ДД, что дает нам 3/14).
Вот почему я включил в название слово «красота». Сочетание некоторых из самых красивых концепций в математике может дать нам такие простые результаты. Let’s recap first what concepts are we talking about and how are we going to combine them:
Euler’s number e
The unit imaginary number i
Pi π
It’s fascinating чтобы увидеть, как эти три вместе образуют уравнение, подобное приведенному ниже, чтобы дать нам простой результат -1.
[источник объяснения: mathsisfun.com]
Как мы получили -1 от трех мушкетеров?
Как мы уже вместе видели, я возвел в степень 2 = -1. Леонард Эйлер применил ряд Тейлора, дав ему следующее уравнение (опуская детали, поскольку они выходят за рамки этой статьи): круг. Включив радиус r, мы можем преобразовать точки в другую форму, такую как re в степени ix .
Если принять x = π , то мы будем иметь следующее:
Зная, что cos π = -1 и sin π = 0, то i справа исчезнет:
Итак, мы также можем изменить это уравнение, чтобы сделать его более красивым, и добавить еще одно простое число:
Также известное как константа Капрекара, это число имеет особую особенность, если вы выполните следующие шаги (взято из разных источников, но скажем, из Википедии):
Возьмем любое четырехзначное число (хотя бы две цифры должны отличаться).
Расположите цифры в порядке убывания и возрастания , чтобы получить два новых четырехзначных числа.
Теперь вычтите меньшее число из большего числа.
Повторить шаг 2.
Если вы сделаете это для нескольких шагов, вы всегда получите 6174 , и это загадочная вещь. Почему мы всегда заканчиваем этим числом, независимо от того, с каких чисел вы начинаете. Возьмем пример 2714:
7421 -1247 = 6174
Другой пример 3687:
8763 -3678 = 5085;
8550 -0558 = 7992;
9972 -2799 = 7173;
7731 -1377 = 6354;
6543 -3456 = 3087;
8730 -0378 = 8352;
8532 -2358 = 6174
Теперь, если у нас есть 6174 , мы всегда будем оставаться на 6174 , потому что 7641 -1467 = 0074 6174.
Это также число Харшада, означающее, что оно делится на сумму своих составляющих: 6174 / (6 + 1 + 7 + 4) = 6174 / 18 = 343. Так что это добавляет ему крутости.
Мы уже обсуждали это соотношение, но это, вероятно, самое важное соотношение в мире (Его назвали греки). Вот список его характеристик:
Обратное число 0,618 равно 1 + 0,618 . Следовательно, 1 / ϕ ≈ 1 + ϕ
Он появляется в Nature (как упоминалось ранее). Например, некоторые ветки деревьев. Основной ствол будет расти до тех пор, пока не создаст ответвление, создав таким образом две новые отправные точки. Одна из отправных точек вырастет двумя другими, а другая — нет. Паттерн похож на паттерн Фибоначчи.
Источник: https://in.pinterest.com/pin/415034921892322849/
Считается, что он представляет собой Красота , и хотя это мнение не доказано, по-прежнему интересно узнать, как наш разум определяет красоту. Например, лицо. Следующее, вероятно, не является самым точным исследованием, но доктор Шмид имеет 10-кратное соотношение по шкале, где 10 является самым высоким (самый красивый человек), а большинство людей получают от 4 до 6. Метрика красоты сначала измеряется длиной и ширина лица затем делится на ширину. Оптимальный результат 1,618. Это означает, что лицо красивого человека в 1,618 раза длиннее его ширины. Позже рассчитываются другие отношения, такие как нижняя часть носа к нижней части подбородка. Наконец, выполняются тесты на симметрию, чтобы проверить больше показателей красоты. Доктор Шмид говорит, что длина уха должна быть равна длине носа на идеальном лице, среди прочих характеристик.
Считается, что отношение нашей руки к нашему переду равно ϕ .
Присутствует в Геометрия. Многие здания и произведения искусства имеют золотое сечение. Примером может служить Парфенон в Греции.
Внутри пантаграммы встроено золотое сечение.
Источник информации: vsauce.
Недавно я начал собирать NFT для поддержки различных гуманитарных и медицинских целей. Общество Света — это набор ограниченных предметов коллекционирования, которые помогут сделать мир немного лучше, так как при каждой продаже процент от этого будет отправлен непосредственно на благотворительность, связанную с аватаром. Как я всегда говорю, нет ничего лучше, чем маркированный список, чтобы обозначить преимущества покупки этих NFT:
Высокая потенциальная прибыль : Концентрируя оставшиеся средства от продаж на маркетинге и продвижении Общество Света , я стремлюсь максимально увеличить их стоимость на вторичном рынке. Помните, что торговля на вторичном рынке также означает, что часть роялти будет передана той же благотворительной организации.
Коллекция произведений искусства и диверсификация портфолио : Иметь коллекцию аватаров, символизирующих добрые дела, действительно приятно. Инвестирование не обязательно должно быть связано только с эгоистичными потребностями, хотя нет ничего плохого в том, чтобы инвестировать, чтобы заработать деньги. Но как насчет того, чтобы инвестировать в , чтобы зарабатывать деньги, помогать другим и коллекционировать произведения искусства?
Пожертвования на ваши любимые цели: Это гибкий способ выделения различных средств на ваши благотворительные цели.