Дерево пальчиковое – Ручное дерево с пальчиковыми листьями

Пальчиковые деревья (часть 2. Операции)

Статья будет состоять из 3х частей:
Пальчиковые деревья (часть 1. Представление)
Пальчиковые деревья (часть 2. Операции)
Пальчиковые деревья (часть 3. Применение)

Пальчиковые Деревья как Последовательности

В первой части статьи мы рассмотрели пальчиковые деревья как перспективную структуру в качестве немутабельных последовательностей. И научились создавать пальчиковые деревья. Хочу заметить, научились создавать так, что стало принципиально невозможно построить неправильные деревья. Теперь наша задача научится работать с пальчиковыми деревьями как с последовательностями: научится присоединять к началу и концу последовательности, научится легко отделять от обоих концов последовательности, а также соединять несколько деревьев в одно.

Мотивацией для разработки этой странной структуры является желание иметь дерево как последовательность, которое позволяло бы быстро иметь доступ к концу и началу. В этой секции мы имплиментируем операции, которые позволяют увидеть в пальчиковых деревьях последовательности.

Присоединение к началу и к концу

Давайте начнём с добавления к началу пальчикового дерева. Идеально, мы хотели бы добавлять элемент просто добавляя его к префиксу дерева. Но это будет работать только для деревьев, которые имеют 1, 2 или 3 элемента в своём префиксе, и совершенно не будет работать для пальчикового дерева, который имеет 4 элемента в своём префиксе. Просто потому, что префикс не может иметь длину более четырёх. Для избежания префикса длиной 5, мы обернём 3 из этих 5 элементов, обернём их в Node используя Branch4 конструкцию, и присоединим их к более глубокому пальчиковому дереву:

-- Используем <| для присоединения к началу. Этот оператор пальчикового дерева аналогичен  : для списков 
infixr 5 <|
(<|) :: a -> FingerTree a -> FingerTree a

-- Базовый случай #1. Если добавляем к пустому пальчиковому дереву, создаём 1 элемент
x <| Empty = Single x

-- Базовый случай #2: Для единичного дерева, расширяем его вглубь на 1
-- Помним, что синтаксис списков на самом деле превращает в 'Affix a' значения
x <| Single y = Deep [x] Empty [y]

-- Рекурсивный случай: если мы имеем префикс из 4х элементов,  мы должны
-- использовать последние 2 элемента с одним новым для того, чтобы создать узел
-- и затем мы добавляем этот узел к более глубокому пальчиковому дереву, который содержит другие узлы
x <| Deep [a, b, c, d] deeper suffix = Deep [x, a] (node <| deeper) suffix
  where
    node = Branch4 b c d
    
-- Нерекурсивный случай: мы всего лишь добавляем к префиксу
x <| tree = tree { prefix = affixPrepend x $ prefix tree }
 

Всё это мы может применить для присоединения справа, поскольку мы имеем такой же самый доступ к правому концу дерева, как и к левому концу:

infixl 5 |>
(|>) :: FingerTree a -> a -> FingerTree a
Empty |> y = Single y
Single x |> y = Deep [x] Empty [y]
Deep prefix deeper [a, b, c, d] |> y = Deep prefix (deeper |> node) [d, y]
  where
    node = Branch4 a b c
tree |> y = tree { suffix = affixAppend y $ suffix tree }
 
 

Теперь мы можем построить пальчиковое дерево легко, используя присоединение к началу и к концу оного.

> let empty = Empty
> 't' <| empty |> 'x' |> 'y' |> 'z' |> 'w' |> 'm'
Deep {prefix = One 't', deeper = Single (Branch4 'x' 'y' 'z'), suffix = Two 'w' 'm'}

Хотя мы реализовали присоединение к началу и концу пальчикового дерева, кажется, что мы не получили много в терминах эффективности из-за деревьев, потому что если мы будем неудачливы и дерево уже будет иметь множество префиксов длиной 4, мы должны обходить глубоко внутрь дерева для добавления элементов. В результате, худший случай добавления к началу и концу — O(lg n), где

Просмотр (Первого и Последнего)

В предыдущем параграфе мы рассмотрели реализацию операции присоединения с начала (|>) и с конца (<|) элементов в Последовательность (sequence), основанного на пальчиковом дереве. Но, кроме добавления элементов, есть острая необходимость посмотреть на них, и удалять их. Обе эти операции основаны на более универсальной операции — просмотре, которую мы ниже реализуем.
Операция просмотра нужна нам в 2х вериях: просмотре справа (viewr) и просмотре слева (viewl). Каждая из них берёт один элемент с конца (левого или правого соответственно) и возвращает элемент вместе с остатком пальчикового дерева.
Для того, чтобы стало более понятно, нам необходим эквивалент следующей функции для списков:

-- Мы возвращаем разделённые значение, внедрённое в `Maybe`,
-- потому что если список или пальчиковое дерево пустое, разделить невозможно.
listViewL :: [a] -> Maybe (a, [a])
listViewL [] = Nothing
listViewL (x:xs) = Just (x, xs)
 

Простейшая реализация для пальчикового дерева может выглядеть так:

-- Для удобства и простоты создадим структуру
-- вместо использования  Maybe (a, FingerTree a).
data View a = Nil | View a (FingerTree a)
  deriving Show

viewl :: FingerTree a -> View a
viewl Empty = Nil                -- Пустую последовательность нельзя просмотреть
viewl (Single x) = View x Empty  -- Остальная часть пуста
viewl (Deep prefix deeper suffix) = 
  View first $ Deep (fromList rest) deeper suffix
  where
    -- Мы знаем, что префикс имеет как минимум один элемент,
    -- поэтому этот шаблон сработает всегда
    first:rest = toList prefix

Мы даже можем протестировать реализацию, как работать с пустым деревом:

> viewl empty
Nil

> viewl exampleTree
View 't' (Deep {prefix = One 'h', deeper = Deep {prefix = Two (Branch3 'i' 's') (Branch3 'i' 's'), deeper = Empty, 
suffix = Two (Branch4 'n' 'o' 't') (Branch3 'a' 't')}, suffix = Three 'r' 'e' 'e'})

И, хотя эта конструкция, кажется, работает, реализация имеет серьёзную утечку. Вы видите её?
Следующий блок кода демонстрирует проблему:

> let View _ rest = viewl exampleTree
> viewl rest
-- аффикс должен иметь от 1 до 4 элементов!

Когда мы пишем этот случай для viewl, который имеет дело с конструктором Deep, мы просто вынимаем элемент из левого префикса. Но это будет работать только для тех пор, пока у нас останется хотя бы 1 элемент, но как только мы захотим вытащить элемент изнутри — дерево будет неправильным. В блоке, описанном выше мы попытались использовать viewl для создания пальчикового дерева, который бы содержал 0 элементов в префиксе, что конечно же нелегально и мгновенно вызовет ошибку.
Поэтому нам необходимо учесть этот случай, и подсчитать количество элементов префиксе пальчикового дерева. Если будет лишь один элемент, мы не можем просто убрать его, вместо этого мы должны использовать viewl для более глубокого пальчикового дерева, чтобы получить ветвь Node a. Этот Node a содержит 2 или 3 значения, поэтому мы может спокойно вытащить один элемент префикса, и вместо этого заменить префиксом, содержащимся в Node a, так что преобразования всегда гарантирует размер аффикса между 1 и 4 элементов. Следующая реализация viewl работает для всех случаев (мы по прежнему используем структуру данных View a, описанную ранее):

-- Простой случай идентичен предыдущего определения
viewl :: FingerTree a -> View a
viewl Empty = Nil                --  Пустую последовательность нельзя просмотреть
viewl (Single x) = View x Empty  -- остальная часть пуста

-- Работать со случаем Deep немного запутанно
-- Когда префикс имеет лишь один элемент
-- существует несколько граничных случаев, которые мы должны учесть
viewl (Deep [x] deeper suffix) = View x rest
  where
    rest =
      -- Считаем остаток пальчикового дерева:
      case viewl deeper of
        -- Если мы имеет узел из более глубокого пальчикового дерева
        View node rest' ->
          -- Заменяем этот узел в префиксе
          Deep (fromList $ toList node) rest' suffix
        
        -- Если же нет более узлов в более глубоком пальчиковом дереве
        -- остаток элементов находится в суффиксе
        -- Нам необходимо перестроить суффикс в пальчиковое дерево
        Nil -> case suffix of
          [x] -> Single x
          [x, y] -> Deep [x] Empty [y]
          
          -- В следующих 2х случаях, мы выбираем все элементы, кроме
          -- одного элемента слева. Единственное
          -- ограничение - каждая сторона имеет по крайней мере по элементу
          [x, y, z] -> Deep [x, y] Empty [z]
          [x, y, z, w] -> Deep [x, y, z] Empty [w]
          
-- Наконец, имеем простой случай с Deep
-- где мы можем всего лишь вытащить элемент из префикса
viewl (Deep prefix deeper suffix) =
  View first $ Deep (fromList rest) deeper suffix
  where
    first:rest = toList prefix

С этой новой реализацией viewl, наш краш-тест отработает на отлично

> let View _ rest = viewl exampleTree
> viewl rest
View 'h' (Deep {prefix = Two 'i' 's', deeper = Deep {prefix = One (Branch3 'i' 's'), deeper = Empty, 
suffix = Two (Branch4 'n' 'o' 't') (Branch3 'a' 't')}, suffix = Three 'r' 'e' 'e'})

Правый вариант viewl, viewr реализован практически полностью аналогично, лишь используя префиксы вместо суффиксов и наоборот.

viewr :: FingerTree a -> View a
viewr Empty = Nil
viewr (Single x) = View x Empty
viewr (Deep prefix deeper [x]) = View x rest
  where
    rest =
      case viewr deeper of
        -- Преобразуем узел в суффикс, если сможем
        View node rest' ->
          Deep prefix rest' (fromList $ toList node)
        
        -- Преобразуем префикс в дерево, если нет больше узлов глубже
        Nil -> case prefix of
          [x] -> Single x
          [x, y] -> Deep [x] Empty [y]
          [x, y, z] -> Deep [x] Empty [y, z]
          [x, y, z, w] -> Deep [x] Empty [y, z, w]
viewr (Deep prefix deeper suffix) =
  View suffixLast $ Deep prefix deeper (fromList suffixInit)
  where
    suffixLast = last $ toList suffix
    suffixInit = init $ toList suffix

Используем функцию точно также, как и viewl, можем просмотреть конец последовательности

> viewr exampleTree
View 'e' (Deep {prefix = Two 't' 'h', deeper = Deep {prefix = Two (Branch3 'i' 's') (Branch3 'i' 's'), deeper = Empty, 
suffix = Two (Branch4 'n' 'o' 't') (Branch3 'a' 't')}, suffix = Two 'r' 'e'})

Так как у нас появились необходимые примитивы для просмотра, мы можем легко создать остальные несколько функций для пальчиковых деревьев, аналогичных head, tail, last, init, и null для списков

treeHead :: FingerTree a -> a
treeHead tree = case viewl tree of
  Nil -> error "no elements in tree"
  View x _ -> x
  
treeTail :: FingerTree a -> FingerTree a
treeTail tree = case viewl tree of
  Nil -> error "no elements in tree"
  View _ xs -> xs

treeLast :: FingerTree a -> a
treeLast tree = case viewr tree of
  Nil -> error "no elements in tree"
  View x _ -> x
  
treeInit :: FingerTree a -> FingerTree a
treeInit tree = case viewr tree of
  Nil -> error "no elements in tree"
  View _ xs -> xs
  
isEmpty :: FingerTree a -> Bool
isEmpty tree = case viewl tree of
  Nil -> True
  _ -> False

И в частности это позволяет нам легко преобразовывать списки в пальчиковые деревья и наоборот:

-- Для удобства будем показывать аффиксы как списки.
instance IsList (FingerTree a) where
  type Item (FingerTree a) = a
  
  toList tree = case viewl tree of
    Nil -> []
    View x xs -> x : toList xs

  fromList = foldr (<|) Empty

Использование пальчиковых деревьев стало значительно более простым:

> [1..6] :: FingerTree Int
Deep {prefix = Two 1 2, deeper = Single (Branch4 3 4 5), suffix = One 6}

Конкатенация

Ещё одну операцию, которую мы можем реализовать используя пальчиковые деревья — это конкатенация/соединение. Для этого у нас есть все необходимые функции для простого соединения, поскольку мы можем рекурсивно просматривать и присоединять элементы. Самой простой реализаций будет:

-- Конкатенацию будем обозначать инфиксным  >< оператором.
(><) :: FingerTree a -> FingerTree a -> FingerTree a
left >< Empty = left
left >< right =
  let View first rest = viewl right in
    (left |> first) >< rest

И хотя эта реализация работает хорошо, эта реализация очень медленная. В терминах асимптотического времени, это то же самое, что использование функции toList разложить пальчиковое дерево, соединить два списка, и преобразовать назад в пальчиковое дерево. Мы ранее показали, что |> занимает O(1) амортизированное время, но данная процедура будет проделана O(m) раз, где m — число элементов в правом дереве, что мы передаём функции ><. В итоге, общее время O(m) — линейно зависит от числа элементов, что мы присоединяем.
Мы попробуем создать значительно лучше, утилизируя структуру пальчикового дерева. Перед тем, как делать это, нам необходима функция-помощник, названная узлами (nodes), которая может преобразовать список элементов в список узлов элементов:

nodes :: [a] -> [Node a]
nodes xs = case xs of
  [] ->  error "not enough elements for nodes"
  [x] -> error "not enough elements for nodes"
  [x, y] -> [Branch3 x y]
  [x, y, z] -> [Branch4 x y z]
  x:y:rest -> Branch3 x y : nodes rest

Для каждых 2х элементов оригинального списка, узлы будут содержать лишь по одному в новом списке узлов. В порядке соединения нечётное количество элементов, узлы будут содержать Branch4 в левой части. Как результат, мы уверены в том, что функция узлов, если ей дать список элементов, всегда создать список из n/2 узлов. Это нам понадобится в дальнейшем.
Далее, мы переопределим конкатенацию в терминах немного странного оператора, который мы назовём «соединить с серединой» (concatWithMiddle). Соединитель берёт два FingerTree a значения для соединения, а также список элементов между двумя деревьями.
Реализовать же соединение с помощью соединителя с серединой — тривиальная задача — всего лишь использовать пустой список в качестве дополнительного аргумента.

(><) :: FingerTree a -> FingerTree a -> FingerTree a
left >< right = concatWithMiddle left [] right

concatWithMiddle :: FingerTree a -> [a] -> FingerTree a -> FingerTree a
concatWithMiddle = unimplemented
  where unimplemented = error "Soon to come!"

Дело за малым — реализовать concatWithMiddle. Нам нужен специальный случай если имеем деревья с конструкторами Empty или Single. В этих случаях соединение редуцируется до O(1) присоединения.
Тут мы храним список из дополнительных элементов посередине также для того, чтобы использовать несколько присоединений с обоих концов.
В дополнение к граничным случаям, мы должны позаботится об основном случае, когда оба дерева имеют конструктор Deep. Здесь мы тоже вернём Deep вместе с:
префиксом, равным префиксу левого дерева,
суффиксом, равным суффиксу правого дерева
глубоким внутренним деревом, равным рекурсивному вызову concatWithMiddle
Мы также должны не забыть о суффиксе левого дерева и префиксе правого дерева. Тем, что мы скомбинируем со средними элементами, переданных concatWithMiddle. В то время, как глубокие пальчиковые деревья хранят узлы Node a вместо а значений, мы используем функцию-помощник для того, чтобы создать список узлов, которые мы передадим рекурсивно функции concatWithMiddle. Это наверняка звучит странно, но должно быть читабельно из кода:

concatWithMiddle :: FingerTree a -> [a] -> FingerTree a -> FingerTree a

-- Базовый случай: просто используем присоединение с одного или другого конца
concatWithMiddle Empty       []    right = right
concatWithMiddle Empty      (x:xs) right = x <| concatWithMiddle Empty xs right
concatWithMiddle (Single y)  xs    right = y <| concatWithMiddle Empty xs right

concatWithMiddle left  [] Empty = left
concatWithMiddle left  xs Empty = concatWithMiddle left (init xs) Empty |> last xs
concatWithMiddle left  xs (Single y) = concatWithMiddle left xs Empty |> y

-- Рекурсивный случай: оба дерева глубокие
concatWithMiddle left mid right = 
  Deep (prefix left) deeper' (suffix right)
  where
    -- Используем concatWithMiddle рекурсивно для того, чтобы генерировать следующий уровень
    deeper' = concatWithMiddle (deeper left) mid' (deeper right)
    
    -- Получаем список элементов в левом суффиксе, имеем середину и правый префикс 
    -- Преобразуем их в узлы до того, как передадим функции concatWithMiddle.
    mid' = nodes $ (toList $ suffix left) ++ mid ++ (toList $ prefix right)

-- Используем >< для более простого соединения.
(><) :: FingerTree a -> FingerTree a -> FingerTree a
left >< right = concatWithMiddle left [] right

Мы можем протестировать, так же, как и ранее, просмотрев как соединяются 2 дерева exampleTree >< exampleTree:

> putStrLn $ toList $ exampleTree >< exampleTree
thisisnotatreethisisnotatree
> putStrLn $ toList $ concatWithMiddle exampleTree " " exampleTree
thisisnotatree thisisnotatree

Хотя понятно, что этот код функционирует (как бы каламбурно это ни звучало), не совсем понятно, что же мы выиграли, и выиграли ли вообще в терминах гарантированного асимптотическое времени исполнения. Если мы посмотрим на базовый случай concatWithMiddle, то всё равно найдём тонну присоединений! Каждый раз заходя рекурсивно внутрь по слою, мы добавляем элементы срединному списку (из неиспользуемых аффиксов). Возможно ли после этого добиться O(m) в базовом случае?
Достаточно неожиданно, ответом будет — нет. Мы можем доказать, что базовый случай всё равно займёт O(1) амортизированное время. Магия тут находится в использовании узлов. Как мы показали, когда определяли функцию узлов, узлы гарантируют выходной список не более половины элементов входного списка. Используя это свойство, мы можем легко отследить, что максимальная длина среднего списка может быть любой во время подсчёта.
Когда подсчёт начинается, мы знаем, что длина среднего списка равна нулю, поскольку передали функции concatWithMiddle пустой список в нашем определении ><. На каждом шаге мы добавляем 2 аффикса (суффикс и префикс) к среднему списку до того как добавляем узлы в него. Мы знаем, что аффиксы имеют не более 4 элементов, а значит, за первую итерацию мы добавим не более 8 элементов, длина на выходе после функции узлов будет близка к 8, но не более 8. Ведь если мы начнём со списка меньше или равным 8 элементов, тогда длину делим пополам, на выходе мы получим снова 8 или меньше элементов. Можно посмотреть на примере, когда начинаем с пустого среднего списка, и будем добавлять 8 элементов за шаг.
Шаг 0. Серединный список пуст, 0 элементов
Шаг 1: Добавляем 8 элементов (4 из суффикса, 4 из префикса). Функция узлов уменьшает длину наполовину, поэтому итоговый список имеет 4 элемента
Шаг 2: Добавляем 8 элементов. Всего 12, узлы сокращают длину до 6
Шаг 3: Добавляем 8 элементов. Всего 14, узлы сокращают длину до 7
Шаг 4: Добавляем 8 элементов. Всего 15, узлы сокращают длину до 7
Заметим, что последние 2 шага оба имели список из одного и того же размера — однажды вычисления достигают предела — средний список достигает длины 7, который O(1) (постоянен), в результате мы можем уверенно говорить, что базовый случай занимает O(1) амортизированное время исполнения, поскольку тут будет не более 8 присоединений.
Так как базовый случай потребят постоянное время, главный, кто вкладывает время в исполнение нашей >< функции, это рекурсия. Каждый рекурсивный шаг, когда мы заглядываем в глубокие деревья обоих правых и левых дерева функции concatWithMiddle, мы переходим к базовому случаю сразу же, когда хотя бы одно из деревьев не будет содержать конструктор Deeper. Глубина этих деревьев растёт логарифмически с ростом элементов в нём, если пальчиковое дерево состоит из n элементов, то глубина его будет O(lg n). А время выполнения пропорциональна минимуму глубины обоих деревьев, наша асимптотическая граница времени будет O(min(lg n,lg m))=O(lg(min(m,n))), где n и m
— количество элементов в правом и левом дереве соответственно.

Что же, в этой части статьи мы научились легко работать с пальчиковыми деревьями как с последовательностями.
Однако потенциал пальчиковых деревьев не исчерпан. В заключительной части статьи мы рассмотрим дополнительные возможности пальчиковых деревьев.

Автор: Vitter

Источник

www.pvsm.ru

Пальчиковые деревья (часть 1. Представление)

Вышла недавно статья на Хабре о том, как можно самому создать на функциональном языке такие структуры как Очередь (первый зашёл, первый вышел) и Последовательность (напоминает двусторонний стек — первый зашёл, первый вышел с обоих концов). Посмотрел я на этот код и понял, что он жутко неэффективен — сложность порядка O(n). Быстро сообразить, как создать структуры с O(1) у меня не вышло, поэтому я открыл код библиотечной реализации. Но там была не лёгкая и понятная реализация, а <много кода>. Это было описание пальчиковых деревьев, необходимость и элегантность которых для этой структуры данных хорошо раскрывается текущей статьёй.

Пальчиковые деревья

В этой статье мы рассмотрим пальчиковые деревья. Это функциональные неизменяемые структуры данных общего назначения, разработанные в работе Гинце и Паттерсона. Пальчиковые деревья обеспечивают функциональную структуру данных Последовательность (sequence), которая обеспечивает амортизированной доступ постоянный во времени для добавления как в начало, так и в конец последовательности, а также логарифмическое время для конкатенации и для произвольного доступа. В дополнение к хорошему времени асимптотических исполнения, структура данных оказывается невероятно гибкой: в сочетании с моноидальными тегами на элементах, пальчиковые деревья могут быть использованы для реализации эффективных последовательностей с произвольным доступом, упорядоченных последовательностей, интервальных деревьев и очередей приоритетов.

Статья будет состоять из 3х частей:
Пальчиковые деревья (часть 1. Представление)
Пальчиковые деревья (часть 2. Операции)
Пальчиковые деревья (часть 3. Применение)

Разрабатывая структуру данных

Основа и мотивация пальчиковых деревьев пришла от 2-3 деревьев. 2-3 деревья — это деревья, которые могут иметь две или три ветви в каждой внутренней вершине и которые имеют все свои листья на одном и том же уровне. В то время, как бинарное дерево одинаковой глубины d должны быть 2^d листьев, 2-3 деревья гораздо более гибкие, и могут быть использованы для хранения любого числа элементов (количество не должно быть степенью двойки).
Рассмотрим следующее 2-3 дерево:

Это дерево хранит четырнадцать элементов. Доступ к любому из них требует трех шагов, и если бы мы должны были добавить больше элементов, количество шагов для каждого из них будет расти логарифмически. Мы хотели бы использовать эти деревья для моделирования последовательности. Тем не менее, во многих применимых последовательностях очень часто и неоднократно обращаются к началу или к концу, и гораздо реже к середине. Для удовлетворения этого пожелания, мы можем изменить эту структуру данных так, чтобы приоритет доступа к началу и к концу был наивысшим в отличие от других особенностей.
В нашем случае, мы добавляем два пальца. Палец просто точка, в которой вы можете получить доступ части структуры данных, в императивных языках это было бы просто указателем. В нашем случае, однако, мы будем реструктуризовать всё дерево и сделаем родителей первых и последних детей двумя корнями нашего дерева. Визуально, рассматривая вопрос об изменении дерева выше, захватываем первый и последний узлы на предпоследнем слое, и тянем их вверх, позволяя остальной части дерева свисать: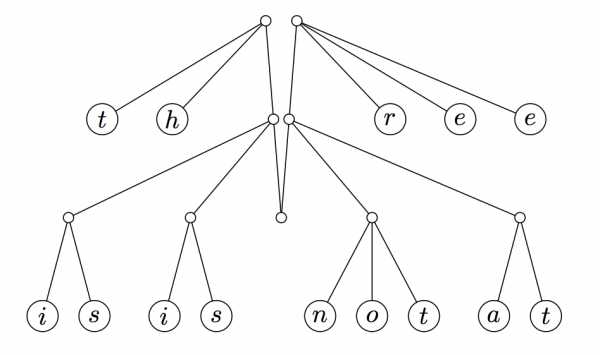


Этот новый тип данных известен как пальчиковое дерево. Пальчиковое дерево состоит из нескольких слоёв (обведенные синим цветом), которые нанизаны на ось, показанную коричневым цветом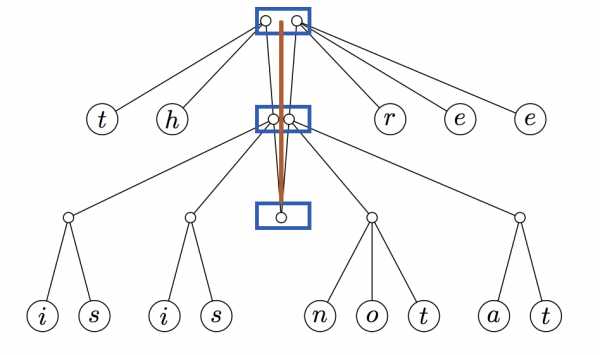

Каждый слой пальчикового дерева имеет префикс (слева) и суффикс (справа), а также и ссылку на дальнейший поход вглубь. Префикс и суффикс содержат значения пальчикового дерева: на первом слое содержат значения 2-3 деревьев глубины 0, на втором слое — 2-3 деревья глубины 1, на третьем слое они содержат 2-3 деревья глубины 2 и так далее. Главным элементом этого 2-3 дерева сейчас является элемент в самом низу.
Что ж, имея описание, давайте опишем структуру данных. Для начала мы должны определить структуру 2-3 дерева, которую необходимо будет использовать для сохранения вещей, нанизанных на ось.

data Node a = Branch4 a a a    -- Ветка (node) может содержать 3х детей.
            | Branch3 a a      -- ... или только 2х детей.
            deriving Show

Заметим, что ветка параметризована по своим детям. Это позволяет иметь вложенные ветки для репрезентации 2-3 деревьев и гарантировать одинаковость глубины. Например, 2-3 дерево глубиной 1 может быть Node Char:

> -- 2-3 деревья со 2го суффиксного слоя экземпляра пальчикового дерева.
> Branch4 'n' 'o' 't'
Branch4 'n' 'o' 't'
> Branch3 'a' 't'
Branch3 'a' 't'

Однако, мы можем также создать более глубокие 2-3 деревья. Например, 2-3 дерево, глубиной 2 может быть Node (Node Char):

> Branch3 (Branch4 'n' 'o' 't') (Branch3 'a' 't')
Branch3 (Branch4 'n' 'o' 't') (Branch3 'a' 't')

Замечаем, что отображение гарантирует, что 2-3 дерево будет одинаковой глубины, потому что глубина присутствует в типе дерева. Это так же имеет свои недостатки, так как сложнее писать функции, которые параметрические по параметру глубины дерева. Но это не так плохо для нашего случая.
Для дальнейшего нашего удобства, добавим немного методов, которые позволят нам преобразовывать значения веток из списков длиной 2 или 3. Для этого будем использовать расширение OverloadedLists для GHC, которое позволит нам написать функции fromList и toList для различных типов данных, и далее использовать их для сравнений с образцом, если мы используем списки:

{- LANGUAGE OverloadedLists, TypeFamilies -}
import GHC.Exts (IsList(..))

instance IsList (Node a) where
  type Item (Node a) = a
  
  toList (Branch3 x y)   = [x, y]
  toList (Branch4 x y z) = [x, y, z]
  
  fromList [x, y]    = Branch3 x y
  fromList [x, y, z] = Branch4 x y z
  fromList _ = error "Node must contain two or three elements"

Теперь, когда мы имеем наш тип 2-3 дерева, необходим также тип для сохранения префикса и суффиксов, которые нанизаны на ось пальчикового дерева. Если наше пальчиковое дерева является полной аналогией 2-3 дерева, тогда каждые самые первые префиксы и суффиксы могут иметь 2 или 3 элемента, а средние могут иметь только 1 или 2 (потому что один из ссылок идёт вверх на один уровень вверх по оси). Однако, для уменьшения информативности, требование ослаблено для пальчиковых деревьев, и, вместо этого, каждый префикс и суффикс содержат от 1 до 4 элементов. Больше значений быть не может. Мы могли бы позволить сохранять префикс и суффикс в виде списков, но мы вместо этого будем использовать более селективные конструкторы, каждый из которых отвечает за своё правильное количество элементов:

-- Параметризуем аффикс типом данных, который он сохраняет
-- Тип эквивалентен спискам длиной от 1 до 4
data Affix a = One a
             | Two a a
             | Three a a a
             | Four a a a a
             deriving Show

Работать с таким типом данных не так уж и удобно, поэтому мы быстро допишем функции-помощники, которые позволяют работать с аффиксами как со списками.

-- Работам с аффиксами как со списками
instance IsList (Affix a) where
  type Item (Affix a) = a
  
  toList (One x)        = [x]
  toList (Two x y)      = [x, y]
  toList (Three x y z)  = [x, y, z]
  toList (Four x y z w) = [x, y, z, w]
  
  fromList [x]          = One x
  fromList [x, y]       = Two x y
  fromList [x, y, z]    = Three x y z
  fromList [x, y, z, w] = Four x y z w
  fromList _ = error "Affix must have one to four elements"
  
-- Следующая функция может быть куда более эффективной
-- Мы же будем использовать самую простую реализацию на сколько возможно
affixPrepend :: a -> Affix a -> Affix a
affixPrepend x = fromList . (x :) . toList

affixAppend :: a -> Affix a -> Affix a
affixAppend x = fromList . (++ [x]) . toList

Теперь, когда мы определили тип данных, необходимых для хранения значений (2-3 деревья, сохраняющие значения и аффиксы, прикрепленные к оси), мы можем создать осевую структуру данных. Эта осевая структура и есть то, что мы называем пальчиковым деревом, и определяется она так:

-- Как обычно, параметрезируется тип тем типом, который он сохраняет в пальчиковом дереве
data FingerTree a 
  = Empty      -- Дерево может быть пустым
  | Single a   -- Дерево может содержать единственное значение, удобно это записать в отдельный случай
  
  -- Общий случай с префиксом, суффиксом и ссылкой на вглубь дерева
  | Deep {
    prefix :: Affix a,             -- Значения слева
    deeper :: FingerTree (Node a), -- Более глубокая часть пальчикового дерева, хранящая 2-3 деревья
    suffix :: Affix a              -- Значения справа
  }
  deriving Show

В определении выше, глубокое поле FingerTree a имеет тип FingerTree (Node a). Это означает, что значения, хранимые на следующем слое являются 2-3 деревьями, которые находятся на уровень глубже. Так, аффиксы первого слоя FingerTree Char хранят всего лишь Char, второй слой хранит FingerTree (Node Char) и имеет аффиксы, которые хранят 2-3 деревья глубиной 1 (Node Char). Третий слой будет уже FingerTree (Node (Node Char)) и имеет аффиксы, которые хранят 2-3 деревья глубиной 2 (Node (Node Char)).

Сейчас, когда мы определили наш тип пальчикового дерева, проведём немного больше времени и рассмотрим примет, который был показан выше, для того, чтобы понять как мы переводим его в структуру FingerTree Char: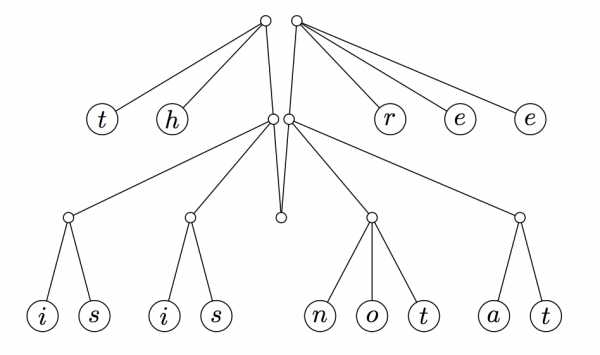

Переведя это в дерево, получим:

layer3 :: FingerTree a
layer3 = Empty

layer2 :: FingerTree (Node Char)
layer2 = Deep prefix layer3 suffix
  where
    prefix = [Branch3 'i' 's', Branch3 'i' 's']
    suffix = [Branch4 'n' 'o' 't', Branch3 'a' 't']

layer1 :: FingerTree Char
layer1 = Deep prefix layer2 suffix
  where
    prefix = ['t', 'h']
    suffix = ['r', 'e', 'e']

exampleTree :: FingerTree Char
exampleTree = layer1

> exampleTree
Deep {prefix = Two 't' 'h', deeper = Deep {prefix = Two (Branch3 'i' 's') (Branch3 'i' 's'), deeper = Empty, 
suffix = Two (Branch4 'n' 'o' 't') (Branch3 'a' 't')}, suffix = Three 'r' 'e' 'e'}

В следующей части статьи мы научимся легко работать с пальчиковыми деревьями как с последовательностями.

Автор: Vitter

Источник

www.pvsm.ru

Пальчиковые деревья — Рубрика — PVSM.RU

Вышла недавно статья на Хабре о том, как можно самому создать на функциональном языке такие структуры как Очередь (первый зашёл, первый вышел) и Последовательность (напоминает двусторонний стек — первый зашёл, первый вышел с обоих концов). Посмотрел я на этот код и понял, что он жутко неэффективен — сложность порядка O(n). Быстро сообразить, как создать структуры с O(1) у меня не вышло, поэтому я открыл код библиотечной реализации. Но там была не лёгкая и понятная реализация, а <много кода>. Это было описание пальчиковых деревьев, необходимость и элегантность которых для этой структуры данных хорошо раскрывается текущей статьёй.

Пальчиковые деревья

В этой статье мы рассмотрим пальчиковые деревья. Это функциональные неизменяемые структуры данных общего назначения, разработанные в работе Гинце и Паттерсона. Пальчиковые деревья обеспечивают функциональную структуру данных Последовательность (sequence), которая обеспечивает амортизированной доступ постоянный во времени для добавления как в начало, так и в конец последовательности, а также логарифмическое время для конкатенации и для произвольного доступа. В дополнение к хорошему времени асимптотических исполнения, структура данных оказывается невероятно гибкой: в сочетании с моноидальными тегами на элементах, пальчиковые деревья могут быть использованы для реализации эффективных последовательностей с произвольным доступом, упорядоченных последовательностей, интервальных деревьев и очередей приоритетов.

Статья будет состоять из 3х частей:
Пальчиковые деревья (часть 1. Представление)
Пальчиковые деревья (часть 2. Операции)
Пальчиковые деревья (часть 3. Применение)

Разрабатывая структуру данных

Основа и мотивация пальчиковых деревьев пришла от 2-3 деревьев. 2-3 деревья — это деревья, которые могут иметь две или три ветви в каждой внутренней вершине и которые имеют все свои листья на одном и том же уровне. В то время, как бинарное дерево одинаковой глубины d должны быть 2^d листьев, 2-3 деревья гораздо более гибкие, и могут быть использованы для хранения любого числа элементов (количество не должно быть степенью двойки).
Рассмотрим следующее 2-3 дерево:

Это дерево хранит четырнадцать элементов. Доступ к любому из них требует трех шагов, и если бы мы должны были добавить больше элементов, количество шагов для каждого из них будет расти логарифмически. Мы хотели бы использовать эти деревья для моделирования последовательности. Тем не менее, во многих применимых последовательностях очень часто и неоднократно обращаются к началу или к концу, и гораздо реже к середине. Для удовлетворения этого пожелания, мы можем изменить эту структуру данных так, чтобы приоритет доступа к началу и к концу был наивысшим в отличие от других особенностей.
В нашем случае, мы добавляем два пальца. Палец просто точка, в которой вы можете получить доступ части структуры данных, в императивных языках это было бы просто указателем. В нашем случае, однако, мы будем реструктуризовать всё дерево и сделаем родителей первых и последних детей двумя корнями нашего дерева. Визуально, рассматривая вопрос об изменении дерева выше, захватываем первый и последний узлы на предпоследнем слое, и тянем их вверх, позволяя остальной части дерева свисать:

Читать полностью »

www.pvsm.ru