Фрактал Ньютона | Компьютерная графика
Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения f(z)=0 алгоритмом Ньютона на комплексной плоскости. Для функции действительной переменной метод Ньютона часто называют методом касательных. Поясним суть этого метода.
Пусть нам задана функция f(x), для которой известно приближенное значение ее корня x1, а также значение функции в этой точке f(x1) и значение её первой производной f ‘(x1). Тогда, проводя касательную к графику функции f(x) в этой точке и определяя ее пересечение с осью Ox, мы получим уточненное положение корня x2.
Т. к. уравнение касательной к f(x) в точке x1 выглядит следующим образом:
y=f ‘(x1)(x-x1)+f(x1),
то, приравнивая y нулю, получаем, что уточненное значение корня x
x2=x1-f(x1)/f ‘(x1)
Беря теперь значение x в качестве приближенного и повторяя эту процедуру, находим следующее приближение корня x3 и т.д. При некоторых условиях эта последовательность сходится к корню уравнения f(x)=0. Рассмотрим теперь комплексный случай. Рассмотрим уравнение f(z)=0 и последовательность
zn+1=zn-f(zn)/f ‘(zn)
Пусть f(z)=z3-1. Как известно, это уравнение имеет три корня ω1, ω2, ω3. При выборе различных z0 процесс будет сходится к различным корням. Обозначим эти области притяжения через A(ωi)={z0 | zn→ωi}. Артур Кэли поставил задачу описания областей A(ωi ). Оказывается границы этих областей имеют фрактальную структуру.
grafika.me
Фрактал Ньютона | Основы программирования
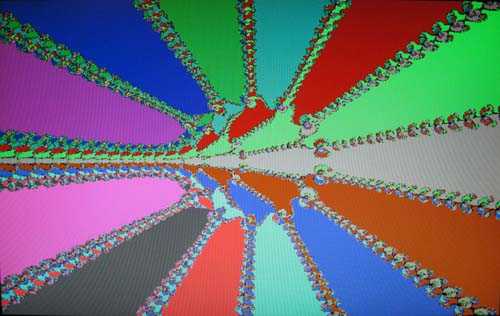
Бассейны Ньютона, фракталы Ньютона — разновидность алгебраических фракталов.
Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости.
История и дополнительные сведения о фрактале http://ru.wikipedia.org/wiki/Бассейны_Ньютона
Алгоритм
В данном случае рассматривается полином как функция комплексного переменного.
zn+1 = zn — f(zn) / f'(zn)
1. Задается степень полинома, массив его коэффициентов, количество итераций, погрешность.
2. Вычисляется начальное приближение z0 = xmin + ymin * i;
3. Далее в цикле с помощью процедуры описанной выше находятся нули функции,
пока не будет достигнута требуемая погрешность для приближенного корня или заданное количество итераций.
В архиве 2 файла :
complex.c — простая структура для работы с комплексными числами
nf.c — основная программа
#include <stdio.h>
#include <math.h>
#include <conio.h>
#include <dos.h>
#include <stdlib.h>
#include <graphics.h>
#include "complex.c"
#define EE 1E-80
#define MAX_ROOTS 15
#define BGI_PATH "C:\\Lang\\BCLite\\BGI"
typedef struct
{
Complex root[MAX_ROOTS];
int nor; // number of root
int deg; // degree
} Roots;
// возвращает номер корня полинома для заполнения области
int process_root(Complex z, Roots *p, float EPS)
{
int i;
for(i=0; i < p->nor; i++)
if (mod( csub( z, p->root[i] ) ) < EPS)
return i+1;
p->root[p->nor]=z;
p->nor+=1;
return p->nor;
}
// инициализация корней
void Rootinit(Roots *roots)
{
register int i;
for(i=0;i<MAX_ROOTS;i++)
roots->root[i]=comp(0,0);
roots->nor=0;
roots->deg=0;
}
// возвращает значение полинома в точке z
Complex f(Complex z, int deg, float poly[])
{
register int i;
register Complex f;
f=comp(poly[deg],0);
for(i=deg-1; i>=0; i--)
f=cadd( cmult(f,z), comp(poly[i],0) );
return f;
}
// возвращает значение первой производной полинома в точке z
Complex df(Complex z, int deg, float poly[])
{
register int i;
register Complex df;
df=comp(deg*poly[deg],0);
for(i=deg-1; i>0; i--)
df=cadd( cmult(df,z), comp(i*poly[i],0) );
return df;
}
void Initialize()
{
int gd, gm, errorcode;
gd = DETECT;
initgraph(&gd, &gm, BGI_PATH);
errorcode = graphresult();
if (errorcode != grOk) /* an error occurred */
{
printf("Graphics error: %s\n", grapherrormsg(errorcode));
printf("Press any key to halt:");
getch();
exit(1); /* return with error code */
}
}
int drawFrac(float dx, float per, float poly[], int deg, int NIT, float EPS)
{
float dy, xmin, ymin, x, y;
int X,Y;
int ITEST;
int i,j,k,kit,col; // счетчики, кол-во итераций, цвет
Complex z,w,fz,dfz;
Roots roots;
FILE *fp;
Rootinit(&roots);
roots.deg = deg;
Initialize();
per = sqrt(per/100);
//per *= 0.01;
// масштаб
X = getmaxx()*per;
Y = getmaxy()*per;
dy= (dx*Y)/X;
xmin = -dx;
ymin = dy;
for(i=0; i<=Y; i++)
{
y = ymin - 2*i*dy/Y;
for(j=0; j<=X; j++)
{
x = xmin + 2*j*dx/X;
z=comp(x,y);
ITEST=1;
// цикл до тех пор, пока не достигнем нужного числа итераций,
// или не найдем максимально близкий корень
for(k=1; k<=NIT; k++)
{
kit=k;
fz = f(z,roots.deg,poly);
dfz = df(z,roots.deg,poly);
if ( mod(dfz)<=EE ) { ITEST=0; break;}
w=z;
z=csub( z, cdiv(fz,dfz) ); // zn+1 = zn - f(zn)/f'(z)
if( mod( csub(z,w) ) <= EPS) break;
}
if (kit == NIT) ITEST=2;
if (ITEST != 1) putpixel(j,i,BLACK);
else
{
col = process_root(z,&roots,EPS);
putpixel(j,i,col);
}
}
if ( kbhit() != 0) break;
}
while(!kbhit()){ }
restorecrtmode();
getch();
return 0;
}
void main(void)
{
char answ;
float poly[MAX_ROOTS+1]={-1,0,0,0,0,1,0};
float dx=2,per=20;
float EPS=1E-10;
int i,deg=5,NIT=40;
do
{
clrscr();
printf("INPUT TO DRAW FRACTAL\n");
printf("1) Polynominal degree (max is %d) : \t%d\n",MAX_ROOTS,deg);
printf(" Coeficients : \n");
for(i=deg;i>=0;i--) printf("\t\tA%d= %f\n",i,poly[i]);
printf("2) Width of the area on the cartesian surface (dx) : \t%f\n",dx);
printf("3) Percentage of the area of the screen to be covered: \t%f\n",per);
printf("4) Maximum Number of Iterations : \t\t\t%d\n",NIT);
printf("5) Precision : \t\t\t\t\t\t%G \n",EPS);
printf("6) Draw Fractal\n");
printf("7) Exit \n");
printf("\nWhat is your choice ? ");
answ=getch();
clrscr();
switch (answ)
{
case('1'):
do
{
printf("\nEnter the degree of the complex polynominal [<=%d]: ",MAX_ROOTS);
scanf("%d",°);
}while (deg>15 || deg<0);
printf("\nEnter the coeficients starting with the greatest power\n");
for(i=deg;i>=0;i--)
{
printf("A%d = ",i);
scanf("%f",&poly[i]);
}
break;
case('2'):
do
{
printf("\nEnter the width (dx>0) = ");
scanf("%f",&dx);
}while(dx<=0);
break;
case('3'):
do
{
printf("\nEnter the percentage of the screen to be covered by the fractal(%)\n");
printf("(the smallest the fastest ->useful for a preview) : ");
scanf("%f",&per);
}while (per<=0 || per>100);
break;
case('4'):
do
{
printf("\nEnter the maximum Number of ITerations (NIT>0) : ");
scanf("%d",&NIT);
}while(NIT<=0);
break;
case('5'):
do
{
printf("\nEnter precision ( >0 ) : ");
scanf("%e", &EPS);
}while (EPS<0);
break;
case('6'):
drawFrac(dx,per,poly,deg,NIT,EPS);
break;
case('7'):
exit(0);
} /*end switch */
} while(1); /*end do-loop*/
} 
| Вложение | Размер |
|---|---|
| Nfrac.rar | 2.58 кб |
www.opita.net
Интерполяция полиномом Ньютона | Компьютерная графика
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace Newton_Interpolate
{
public partial class Form1 : Form
{
public struct point //Структура точки
{
public double X, Y; //Машинные координаты
public double x, y; //Реальные координаты
}
//Координаты исходных точек.
public double[,] Pts = { { -10, 18.7 },
{ -8, 10.3 },
{ -4.5, -5.2 },
{ -2.2, -4 },
{ 0, 4.2},
{4.2, 2.9},
{6.4, 3.6},
{8.6, 4.7},
{10, 10.2}
};
public point[] Points = new point[100]; //Массив точек
public Font drawFont = new Font("Arial", 8); //Стиль шрифта и его размер, для отрисовки координат точек на плоскости
public int xc=300, yc=300; //Координаты центра координатных осей
public Form1()
{
InitializeComponent();
}
//Отрисовка плоскости, с точками и координатными осями
public void drawPlain()
{
Graphics g = Graphics.FromHwnd(picturebox1.Handle);
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
g.Clear(Color.Black);
Pen Axis = new Pen(Color.White, 1);
g.DrawLine(Axis, 0, 300, 600, 300);
g.DrawLine(Axis, 300, 0, 300, 600);
for (int i = 0; i <= 600; i += 15)
{
g.DrawLine(Axis, i, 298, i, 302);
g.DrawLine(Axis, 298, i, 302, i);
}
for (int i = 0; i < (Pts.Length / 2); i++)
{
Points[i].x = Pts[i, 0];
Points[i].y = Pts[i, 1];
Points[i].X = xc + Points[i].x * 15;
Points[i].Y = yc - Points[i].y * 15;
}
DrawPoints();//Отрисовка точек
}
public int ChangeCoordinates(double a, int isY) //Перевод координат из реальных в машинные
{
if (isY == 1) return (int)(yc - a * 15);
return (int)(xc + a * 15);
}
//Высчитывание полинома Ньютона в заданном отрезка, с заданными точками.
public double Newton(double x)
{
double res = Points[0].y, F = 0, den = 1, n = Pts.Length/2;
int i, j, k;
for (i = 1; i < n; i++)
{
F = 0;
for (j = 0; j <= i; j++)
{
den = 1;
for (k = 0; k <= i; k++)
{
if (k != j) den *= (Points[j].x - Points[k].x);
}
F += Points[j].y / den;
}
for (k = 0; k < i; k++) F *= (x - Points[k].x);
res += F;
}
return res;
}
//Отрисовка точек и их координат на плоскости
public void DrawPoints()
{
Graphics g = Graphics.FromHwnd(picturebox1.Handle);
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
SolidBrush pointBrush = new SolidBrush(Color.Green);
SolidBrush drawPointBrush = new SolidBrush(Color.Cyan);
for (int i = 0; i < (Pts.Length / 2); i++)
{
g.FillEllipse(pointBrush, (float)Points[i].X - 2, (float)Points[i].Y - 2, 4, 4);
String drawString = "[" + Points[i].x + "; " + Points[i].y + "]";
PointF drawPoint = new PointF((float)Points[i].X, (float)Points[i].Y);
g.DrawString(drawString, drawFont, drawPointBrush, drawPoint);
}
}
//Отрисовка интерполированной функции по нажатию на кнопку "Draw"
private void Draw_Button_Click(object sender, EventArgs e)
{
Graphics g = Graphics.FromHwnd(picturebox1.Handle);
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
SolidBrush drawLineNewton = new SolidBrush(Color.Red);
drawPlain();
for (double i = -15.0f; i <= 15.0f; i += 0.0005f)
{
g.FillEllipse(drawLineNewton, ChangeCoordinates(i, 0), ChangeCoordinates(Newton(i), 1), 1, 1);
}
DrawPoints();
}
}
} grafika.me
Яблоня, вошедшая в историю мировой науки
Вулсторп Манор – имение Ньютона в Линкольншире, Англия.
Большую часть своих открытий в разных областях механики, оптики и математики молодой ученый Исаак Ньютон совершил в период 1665-1667 гг. В это время в Англии бушевала пандемия чумы, Кембриджский университет был закрыт, и Ньютон пережидал опасность в своем имении, где он родился и вырос. Именно в Вулсторп Манор (Woolsthorpe Manor) в Линкольншире в саду растет дерево, ставшее притчей во языцех.
Дерево, с которого упало знаменитое яблоко.
Этой яблоне уже около 400 лет. Последние же 240 лет дерево страдает от наплыва туристов, которые утрамбовывают под ним землю и срывают ветки на память. Многие даже сидят под ним, ожидая, что очередное яблоко свалится на них сверху.
Согласно легенде, молодой Исаак Ньютон прогуливался по саду, размышляя о природе физических явлений. И вдруг с ветки дерева оторвалось яблоко и упало ему на голову. Якобы в тот же миг Ньютону пришла светлая мысль о силе притяжения.
Вольтер – французский философ-просветитель, поэт, драматург, прозаик XVIII века.
Такую версию событий впервые изложил в 1728 году философ и писатель Вольтер. Великий француз был популяризатором современной ему науки. Он добавил художественных деталей в историю, которую сэр Исаак Ньютон рассказал его племяннице. Так случай с яблоком оказался на страницах книги «Опыт об эпической поэзии».
Однако есть и другая версия события XVIII века, столь значимого для мировой науки. Один из биографов ученого Уильям Стекли в своих «Воспоминаниях о жизни Исаака Ньютона» сообщил несколько другую историю. В частном разговоре Ньютон поведал ему, что яблоко действительно падало. В тот день ученый в задумчивости сидел в саду, а знаменитый плод оторвался от ветки и полетел в траву. Ньютон обратил на это внимание и задался вопросом, почему яблоко упало вниз, а не вверх или в сторону. Возможно, оно переместилось в направлении Земли, которая его притянула. Очевидно, есть сила, которая подействовала на яблоко. Так почему бы этой силе не действовать и дальше, даже до Луны и других планет?
Портрет Исаака Ньютона. Готфрид Кнеллер, 1689 год.
На основании подобных размышлений Исаак Ньютон и сформулировал закон тяготения. Это открытие объясняло очень многие «белые пятна» науки XVIII века, особенно в астрономии. Ученый также прославился своими работами по механике, оптике, дифференциальному и интегральному исчислению. Его труды стали важной составляющей в революции в науке и становлению ее в нынешнем виде.
В наши дни за знаменитой яблоней тщательно ухаживают. Дерево продолжает цвести и плодоносить. Для защиты от толп туристов его оградили небольшим заборчиком, чтобы сохранить корневую систему.
Источник
Примечание Владимира Зыкова. В тему сама просится научная сказка о Ньютоне, написанная автором известной «Астровитянки», учёным Н.Н. Горькавым. Надеюсь, автор простит мне эту публикацию из открытых источников:
Сказка о фермере, открывшем во время чумы законы неба
Жил-был в Англии, на ферме Вулсторп, молодой человек двадцати с небольшим лет. На его ферме было пастбище с овцами, коровник и яблоневый сад. Молодой английский фермер любил сидеть на лавочке под раскидистой яблоней. Фермер из молодого человека, нужно признаться, был никудышный – за обширным хозяйством присматривала мать. А сам юный фермер читал книги и смотрел на солнечные лучи, играющие в яблоневой листве.
В свободное качание листьев на ветерке и в жужжащее мельтешение пчёл часто вмешивалось движение падающих яблок. Они вели себя деловито и одинаково – быстрый полёт к земле и глухой стук. Видно, что они не могли отвлекаться на всякие легкомысленные глупости – у них был приказ, и они его беспрекословно выполняли. Кто отдает им приказ о падении? Ясно, что земной шар с силой притягивает оторвавшиеся от ветки увесистые яблоки. Но как далеко простирается притягивающая воля Земли?
Над яблоневым садом в вечернем небе висит бледная Луна. Притягивает ли Земля Луну на таком расстоянии?
Вот такие странные вопросы задавал себе молодой фермер.
Галилей, чьи книги лежали у фермера на столе, считал, что Земля притягивает яблоки на любых расстояниях и с одинаковой силой. Великий итальянец вычислил, что с высоты Луны яблоко будет падать до Земли три часа и двадцать минут. Но он считал, что Земля не действует на Луну, и наш спутник движется по своим законам. Фермеру эта теория не нравилась – в конце концов, что такое Луна, как не Очень Большое Яблоко? В предположении, что притягивающая сила Земли без ослабления простирается до орбиты Луны, фермер тоже сомневался: ведь воздействие тела – например, магнита – обычно падает с расстоянием.
Вокруг фермы простиралось поле – или пастбище, – сочная трава которого так притягивала соседских коров. Фермер предположил, что вокруг Земли тоже простирается особое поле, которое воздействует на соседние тела. Фермер назвал его гравитационным полем, или полем притяжения, которое действует и на яблоки, и на Луну.
Молодой фермер понимал, что движение Луны сбалансировано (ведь она не падает!), значит, сила притяжения Земли должна уравновешиваться центробежной силой.
Фермер разработал специальный метод математического исчисления и сумел найти выражение для центробежного ускорения Луны – оно оказалось равно квадрату скорости Луны, делённому на радиус лунной орбиты.
Эта простенькая формула для центробежной силы, известная сейчас любому школьнику, была получена английским фермером как раз для движения Луны.
Сегодня сказку детям рассказывала королева Никки, а она не стеснялась в выражениях, особенно – в математических. Рассказывая, она набрасывала на специальной пластине формулы:
Фермер приравнял центробежную силу к гравитационной – и у него получилась формула, которая вычисляла притяжение Земли по скорости движения и радиусу орбиты Луны.
Кеплер уже давно установил соотношение между периодом обращения тел и радиусами их орбит. Поэтому фермер взял формулу Кеплера, выразил период обращения через скорость движения по орбите и получил третий кеплеровский закон в таком виде:
Квадрат скорости орбитального движения спутника падает с ростом радиуса орбиты (математики говорят – обратно пропорционален). То есть, чем больше радиус орбиты спутника, тем медленнее он движется по орбите.
С помощью формулы Кеплера фермер исключил квадрат скоростей из своего уравнения для гравитационной силы.
Никки обратилась к детям:
— Вы знаете третий закон Кеплера и сами легко можете проделать это исключение. У фермера в результате получилось, что притяжение планеты падает с расстоянием как квадрат радиуса орбиты спутника: когда расстояние от планеты вырастает в два раза, сила её притяжения падает в четыре.
Значит, если Луна располагается от центра Земли в 60 раз дальше яблока, то притяжение Луны к Земле должно быть слабее в 60 60 = 3600 раз. Фермер сравнил известное ускорение, с которым двигалась Луна по орбите (0,272 см/сек2) с ускорением падения яблока возле поверхности Земли (981 см/сек2) и с восхищением понял, что они действительно отличаются в 3600 раз!
Английский фермер был поражён красотой и могуществом закона гравитации, который описывал притяжение Солнца и Земли и подчинял себе движение яблока, Луны и всех планет.
Так молодой фермер открыл знаменитый закон всемирного тяготения.
Ещё он понял, что если бросить яблоко с большой скоростью параллельно Земле, то оно облетит вокруг Земли как маленький спутник. Тем самым английский фермер заложил основы будущей космонавтики.
За два года сельской жизни фермер не только основал теорию гравитации и небесную механику, но и разработал новый раздел математики – дифференциальное и интегральное исчисление, а также открыл сокровенную тайну солнечного света, разложив его белый луч на разноцветную радугу.
Молодой фермер открывал одну за другой тайны природы, не думая о публикациях и соперниках, о карьере или инквизиции. Он был беззаботен и увлечён, как мальчик, играющий на берегу океана с красивыми раковинами.
– Что же это за фермер такой, который открывал новые законы один за другим? – спросила удивлённая Галатея.
– Сейчас расскажу о нём подробнее, – Никки хитро улыбнулась. – Его звали Исаак Ньютон, он был сыном фермера и родился в тот год, когда умер Галилей.
Ньютон был нелюдимым, молчаливым мальчиком и в школе учился не очень хорошо, но любил конструировать сложные механизмы, особенно мельницы: водяные, ветряные и даже такие, в которых работали мыши. Но с одной девочкой Ньютон всё-таки подружился. У той было двое хулиганистых братьев, которые ходили в один класс с Ньютоном. После очередной стычки с этими братцами Ньютон решил отомстить и стать им назло самым лучшим учеником класса.
И он добился своей цели!
Благодаря этому в девятнадцать лет Ньютон сумел поступить в колледж в Кембридже и за четыре года обучения стал очень образованным и умным молодым человеком.
В колледже Ньютон увлечённо занимался оптикой, астрономией и математикой, забывая про сон и часто оставляя еду на своей тарелке, поэтому молодой Ньютон был очень худым, а его кошка – очень упитанной.
Студент Ньютон составил себе список из сорока пяти нерешённых проблем в науке и готовился штурмовать их.
Но после получения степени бакалавра Ньютон не стал учёным или преподавателем. Помешала эпидемия чумы, поразившая Лондон. Кембридж попросту закрыли до лучших времен.
23-летнему Ньютону пришлось уехать в деревню, на свою родительскую ферму Вулсторп и стать обычным фермером.
Ферма приносила доход, достаточный для жизни, и оказалась отличным местом для занятий наукой. За два года, проведённых в сельской глуши, очень молодой человек, только что закончивший колледж, совершил революцию в науке.
Открыв закон гравитации, Ньютон и не подумал опубликовать его – молодой Ньютон был слишком нелюдим и слишком мало заботился о славе.
– Тогда он – точно фермер! – решил Андрей.
– После чумы фермер Ньютон вернулся в Кембридж и стал профессором, обучающим студентов. Но и тогда он не подумал опубликовать результаты, полученные им в фермерские годы.
Прошло пятнадцать лет, и в 1682 году в небе появилась яркая комета. Она вызвала живейшие споры среди учёных. Особенно хорошо запомнил год кометы учёный Эдмунд Галлей – ведь его медовый месяц пришелся как раз на этот год. Вскоре Галлей, размышляя о своей «свадебной» комете, пришёл к правильному выводу, что гравитация падает с расстоянием, но не смог вывести из этого закона эллиптичную форму орбит, которую Кеплер предложил для планет и комет.
Но до Галлея дошли слухи, что этими вопросами занимался Ньютон, и он отправился в Кембридж для встречи с ним.
И как же он был потрясён, узнав, что тот уже давным-давно решил эту задачу: вывел закон гравитации и согласовал его с кеплеровскими законами!
В отличие от нелюдимого Ньютона, Галлей был дипломатом. Он сумел уговорить учёного написать книгу о механике небесных тел.
Выпуск книги в те времена всё ещё оставался дорогостоящим делом, и Галлей собирался просить у Королевского научного общества денег на публикацию труда Ньютона.
Но Королевское общество только что выпустило «Историю рыб», которую никто не стал покупать. В результате научное общество осталось без денег.
Галлей был богат и уверен в важности труда Ньютона – и он вложил личные деньги в публикацию книги Ньютона. Королевское общество оказалось настолько бесцеремонным, что предложило Галлею компенсацию в виде пятидесяти экземпляров залежавшейся «Истории рыб»!
В 1687 году трёхтомник «Математические начала натуральной философии» Ньютона увидел свет.
С этой великой книги мировая наука начала новый отсчёт времени. Наступила эпоха математического описания природы. Уравнения пришли в механику и астрономию и превратили их из описательных наук – в точные.
Не только яблоки и планеты, но и кометы подчинились ньютоновской механике.
Ньютон собрал наблюдения о двух дюжинах комет и вычислил орбиту одной из них. Без компьютеров определение орбиты каждой кометы занимало шесть недель расчётов! И нетерпеливый Ньютон сказал Галлею:
– Эдмунд, забирай эти данные и вычисляй остальные орбиты сам!
Галлей был одним из первых астрономов, кто стал применять теорию Ньютона для описания движения небесных тел. Галлей провёл все необходимые расчёты и опубликовал орбиты всех двадцати четырёх комет. При этом он обратил внимание, что орбита кометы, которую он наблюдал вместе со свой молодой женой в 1682 году, очень похожа на орбиты комет, замеченных в 1531 и 1607 годах. Галлей предположил, что кометы 1531, 1607 и 1682 года – не три разные кометы, а одна и та же комета, периодически возвращающаяся к Солнцу. Значит, она должна появиться в следующий раз через 76 лет – в 1758 году.
Предсказание учёного блестяще подтвердилось: комета вернулась в 1758 году, уже после смерти астронома, и была названа кометой Галлея. Её открытие стало триумфом ньютоновской теории тяготения, которая оказалась надёжным инструментом познания мира.
Вот только одну небесную проблему великий Ньютон не решил: он не смог рассчитать движение Луны, на которую действует притяжение не только Земли, но и Солнца.
Между прочим, проблема движения Луны вовсе не была скучной и академической проблемой: она волновала моряков, королей и даже придворных дам.
– Придворные дамы интересовались движением Луны? – удивилась Галатея.
– Да, но об этом вы узнаете из другой истории.
* * *
Катятся санки с горы, взлетают ракеты с космодромов, вращаются планеты вокруг Солнца – движение всех этих и миллионов других тел рассчитывается по уравнениям Ньютона, опубликованным им свыше трёхсот лет назад с помощью Галлея.
Ньютон прожил долгую и плодотворную жизнь учёного, был вознаграждён и научной славой, и высокими должностями. Но он всегда считал своими лучшими годами те, когда он был просто молодым фермером и открывал тайны природы беззаботно и увлечённо.
«Я не знаю, чем кажусь миру; мне же самому кажется, что я был только мальчиком, играющим на берегу моря и развлекающимся тем, что время от времени находил более гладкий камешек или более красивую раковину, чем обыкновенно, в то время как великий океан истины лежал передо мною совершенно неразгаданный».
Примечания для любопытных
Кембриджский университет – один из четырёх старейших университетов мира. Возник в 1209 году на основе собрания учёных города Кембриджа. Представляет собой сообщество многих колледжей. Ньютон учился в Тринити-колледже.
Исаак Ньютон (1642–1727) – великий английский физик, математик, астроном и философ. Его считают самым влиятельным учёным за всю историю земной цивилизации.
Эдмунд Галлей (1656–1742) – английский астроном, открывший периодичность кометы Галлея.
Дифференциальное исчисление – раздел математического анализа, где используется и изучается понятие производной, которое характеризует скорость изменения функции. Процесс вычисления производной называется дифференцированием.
Интегральное исчисление – раздел математического анализа, где используется и изучается понятие интеграла функции, который характеризует площадь, лежащую под графиком функции. Процесс нахождения интеграла называется интегрированием.
kramtp.info
Метод Ньютона — это… Что такое Метод Ньютона?
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.
Описание метода
Обоснование
Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где — сжимающее отображение.
Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда:
В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:
С учётом этого функция определяется выражением:
Эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:
По теореме Банаха последовательность приближений стремится к корню уравнения .
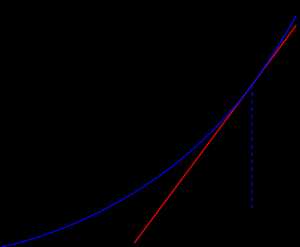
Геометрическая интерпретация
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть — определённая на отрезке и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:
где — угол наклона касательной в точке .
Следовательно искомое выражение для имеет вид:
Итерационный процесс начинается с некоего начального приближения (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).
Алгоритм
- Задается начальное приближение .
- Пока не выполнено условие остановки, в качестве которого можно взять или (то есть погрешность в нужных пределах), вычисляют новое приближение: .
Пример
Рассмотрим задачу о нахождении положительных , для которых . Эта задача может быть представлена как задача нахождения нуля функции . Имеем выражение для производной . Так как для всех и для , очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение , тогда:
Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.
Условия применения
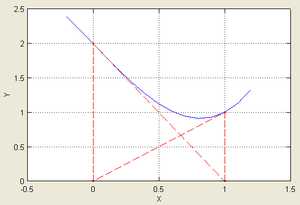Иллюстрация расхождения метода Ньютона, применённого к функции с начальным приближением в точке .Рассмотрим ряд примеров, указывающих на недостатки метода.
Контрпримеры
- Если начальное приближение недостаточно близко к решению, то метод может не сойтись.
Пусть
Тогда
Возьмём нуль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст нуль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.
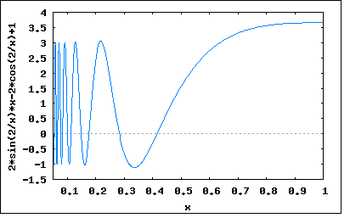График производной функции при приближении к нулю справа.Рассмотрим функцию:
Тогда и всюду, кроме 0.
В окрестности корня производная меняет знак при приближении к нулю справа или слева. В то время, как для .
Таким образом не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.
Рассмотрим пример:
Тогда и за исключением , где она не определена.
На очередном шаге имеем :
Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и бесконечно дифференцируема везде, кроме как в корне.
- Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Пусть
Тогда и следовательно . Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.
Ограничения
Пусть задано уравнение , где и надо найти его решение.
Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).
Теорема Канторовича.
Если существуют такие константы , что:
- на , то есть существует и не равна нулю;
- на , то есть ограничена;
- на , и ;
Причём длина рассматриваемого отрезка . Тогда справедливы следующие утверждения:
- на существует корень уравнения ;
- если , то итерационная последовательность сходится к этому корню: ;
- погрешность может быть оценена по формуле .
Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:
Тогда ограничения на исходную функцию будут выглядеть так:
- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная равномерно отделена от нуля;
- её вторая производная должна быть равномерно ограничена.
Историческая справка
Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения , а последовательность полиномов и в результате получал приближённое решение .
Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.
В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.
Обобщения и модификации
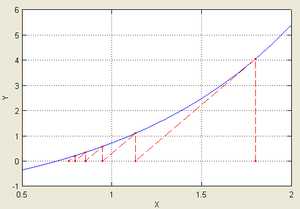Иллюстрация последовательных приближений метода одной касательной, применённого к функции с начальным приближением в точке .Метод одной касательной
В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.
Формула итераций этого метода имеет вид:
Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения , а затем использовать это значение на каждой последующей итерации:
При таком выборе в точке выполнено равенство:
и если отрезок, на котором предполагается наличие корня и выбрано начальное приближение , достаточно мал, а производная непрерывна, то значение будет не сильно отличаться от и, следовательно, график пройдёт почти горизонтально, пересекая прямую , что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.
Этот метод можно также рассматривать, как модернизацию метода хорд (секущих), где число следует выбрать равным
Многомерный случай
Обобщим полученный результат на многомерный случай.
Пусть необходимо найти решение системы:
Выбирая некоторое начальное значение , последовательные приближения находят путём решения систем уравнений:
где .
Применительно к задачам оптимизации
Пусть необходимо найти минимум функции многих переменных . Эта задача равносильна задаче нахождения нуля градиента . Применим изложенный выше метод Ньютона:
где — гессиан функции .
В более удобном итеративном виде это выражение выглядит так:
Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.
Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.
Метод Ньютона — Рафсона
Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:
где Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением и обновляют его лишь раз в шагов, либо не обновляют вовсе.
Применительно к задачам о наименьших квадратах
На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:
Эти задачи отличаются особым видом градиента и матрицы Гессе:
где — матрица Якоби вектор-функции , — матрица Гессе для её компоненты .
Тогда очередное направление определяется из системы:
Метод Гаусса — Ньютона
Метод Гаусса — Ньютона строится на предположении о том, что слагаемое доминирует над . Это требование не соблюдается, если минимальные невязки велики, то есть если норма сравнима с максимальным собственным значением матрицы . В противном случае можно записать:
Таким образом, когда норма близка к нулю, а матрица имеет полный столбцевой ранг, направление мало отличается от ньютоновского (с учётом ), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.
Обобщение на комплексную плоскость
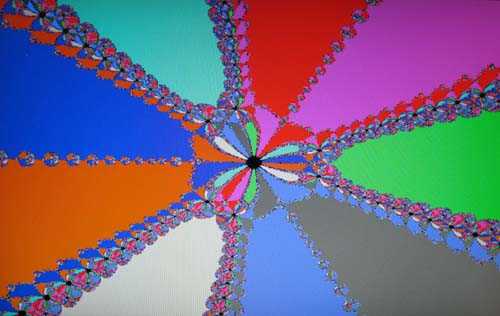
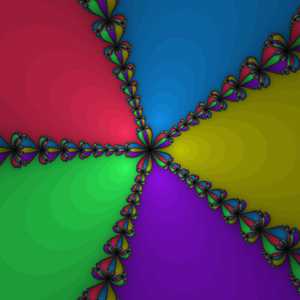Бассейны Ньютона для полинома пятой степени . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций.До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексного переменного. При этом процедура остаётся неизменной:
Особый интерес представляет выбор начального приближения . Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кейли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.
Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.
Литература
- Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. — М.: Мир, 1998.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд.. — М.: Лаборатория Базовых Знаний, 2000.
- Вавилов С. И. Исаак Ньютон. — М.: Изд. АН СССР, 1945.
- Волков Е. А. Численные методы. — М.: Физматлит, 2003.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
- Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
- Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.
Примечания
См. также
Ссылки
dic.academic.ru
Вращающаяся колыбель Ньютона | Компьютерная графика
Язык программирования:
Среда программирования:
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace demoscene1
{
public partial class Form1 : Form
{
private Bitmap bitmap; //инициализируем битмэп
private Graphics graphix; //инициализируем графику
SolidBrush background = new SolidBrush(Color.Blue); //задаем цвет фона
SolidBrush circles = new SolidBrush(Color.White); //задаем цвет кружков
float parameter1, parameter2, parameter3, parameter4, parameter5; //задает вращение кругов
float step; //шаг анимации
float angle; //угол вращения
float x1, y1, x2, y2, x3, y3, x4, y4, x5, y5; //координаты кружков
public Form1()
{
InitializeComponent();
}
private void CirclesLoading()
{
bitmap = new Bitmap(pictureBox1.Width, pictureBox1.Height);
graphix = Graphics.FromImage(bitmap);
graphix.FillRectangle(background, 0, 0, pictureBox1.Width, pictureBox1.Height); //закрашиваем фон
graphix.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias; //сглаживание
graphix.TranslateTransform((float)pictureBox1.Width / 2, (float)pictureBox1.Height / 2); //перемещаем координаты в центр
pictureBox1.BackgroundImage = bitmap; //здесь будет отображаться анимация
}
private void Form1_Load(object sender, EventArgs e)
{
timer1.Start(); //начало работы анимации
}
private void timer1_Tick(object sender, EventArgs e)
{
CirclesLoading(); //загружаем функцию с битмэпом, графикой и отображением анимации
step++; //количество шагов анимации будет постепенно увеличиваться на шаг
angle += (float)0.02262; //изменяем приращение угла
if (step >= 0)
{
x1 = -30 + (float)(180 * (float)Math.Sin(0.20285 + angle + parameter1)); //описываем положение кругов
y1 = -30 + (float)(180 * (float)Math.Cos(0.20285 + angle + parameter1));
x2 = -30 + (float)(180 * (float)Math.Sin(-0.05285 + angle + parameter2));
y2 = -30 + (float)(180 * (float)Math.Cos(-0.05285 + angle + parameter2));
x3 = -30 + (float)(180 * (float)Math.Sin(-0.31295 + angle + parameter3));
y3 = -30 + (float)(180 * (float)Math.Cos(-0.31295 + angle + parameter3));
x4 = -30 + (float)(180 * (float)Math.Sin(-0.55295 + angle + parameter4));
y4 = -30 + (float)(180 * (float)Math.Cos(-0.55295 + angle + parameter4));
x5 = -30 + (float)(180 * (float)Math.Sin(-0.80095 + angle + parameter5));
y5 = -30 + (float)(180 * (float)Math.Cos(-0.80095 + angle + parameter5));
graphix.FillEllipse(circles, x1, y1, 50, 50); //закрашиваем круги
graphix.FillEllipse(circles, x2, y2, 50, 50);
graphix.FillEllipse(circles, x3, y3, 50, 50);
graphix.FillEllipse(circles, x4, y4, 50, 50);
graphix.FillEllipse(circles, x5, y5, 50, 50);
parameter1 += (float)0.16312; //начало движения первого круга
if (step > 31)
{
parameter1 -= (float)0.16312; //прекращение движения первого круга
parameter2 += (float)0.16312; //начало движения второго круга
}
if (step > 62)
{
parameter2 -= (float)0.16312; //прекращение движения второго круга
parameter3 += (float)0.16312; //начало движения третьего круга
}
if (step > 93)
{
parameter3 -= (float)0.16312; //прекращение движения третьего круга
parameter4 += (float)0.16312; //начало движения четвертого круга
}
if (step > 124)
{
parameter4 -= (float)0.16312; //прекращение движения четвертого круга
parameter5 += (float)0.16312; //начало движения пятого круга
}
if (step > 155)
{
parameter5 -= (float)0.16312; //прекращение движения пятого круга
parameter1 += (float)0.16312;
}
if (step > 186)
{
parameter1 -= (float)0.16312;
parameter2 += (float)0.16312;
}
if (step > 217)
{
parameter2 -= (float)0.16312;
parameter3 += (float)0.16312;
}
if (step > 248)
{
parameter3 -= (float)0.16312;
parameter4 += (float)0.16312;
}
if (step > 279)
{
parameter4 -= (float)0.16312;
parameter5 += (float)0.16312;
}
if (step > 310)
{
parameter5 -= (float)0.16312;
parameter1 += (float)0.16312;
}
if (step > 341)
{
parameter1 -= (float)0.16312;
parameter2 += (float)0.16312;
}
if (step > 372)
{
parameter2 -= (float)0.16312;
parameter3 += (float)0.16312;
}
if (step > 403)
{
parameter3 -= (float)0.16312;
}
if (step == 420) //когда анимация дойдет до 420-го шага, то...
{
parameter1 = 0; //обнуляем все счетчики
parameter2 = 0;
parameter3 = 0;
parameter4 = 0;
parameter5 = 0;
angle = 0;
step = 0;
}
}
}
}
}| Прикрепленный файл | Размер |
|---|---|
| zakharov_demoscene1.zip | 54.58 кб |
grafika.me
Фрактал Ньютона | Компьютерная графика
Среда программирования:
Статья по теме:
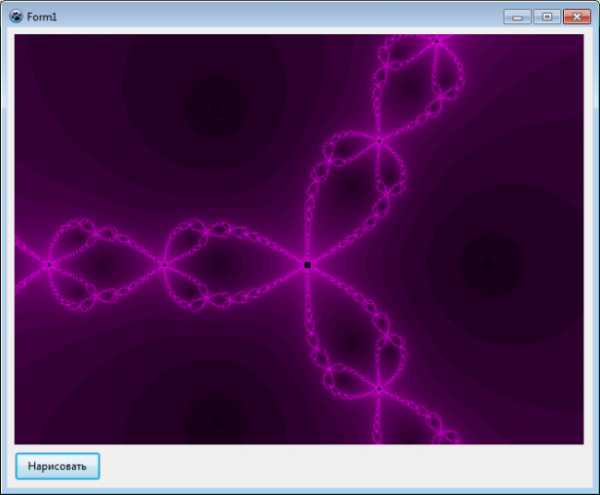
Бассейны Ньютона, фракталы Ньютона — разновидность алгебраических фракталов.
Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости (для функции действительной переменной метод Ньютона часто называют методом касательных, который, в данном случае, обобщается для комплексной плоскости).
Код программы:
unit Unit1;
{$mode objfpc}{$H+}
interface
uses
Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls,
ExtCtrls;
type
{ TForm1 }
TForm1 = class(TForm)
Button1: TButton;
PaintBox1: TPaintBox;
procedure Button1Click(Sender: TObject);
private
{ private declarations }
public
{ public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.lfm}
{ TForm1 }
procedure TForm1.Button1Click(Sender: TObject);
type
Complex = Record
x : Real;
y : Real;
end;
const
iter = 50;
max = 1e+6;
min = 1e-6;
var
z, t, d : Complex;
p : Real;
x, y, n : Integer;
Cancel : Boolean;
gd, gm : Smallint;
mx, my : Integer;
col: TColor;
begin
Randomize;
PaintBox1.Canvas.Clear;
Mx := PaintBox1.Canvas.Width div 2;
My := PaintBox1.Canvas.Height div 2;
for y := -my to my do
for x := -mx to mx do
begin
n := 0;
z.x := X * 0.005;
z.y := Y * 0.005;
d := z;
while (sqr(z.x)+sqr(z.y) < max) and (sqr(d.x)+sqr(d.y) > min)
and (n < iter) do
begin
t := z;
{z^3 - 1}
p := sqr(sqr(t.x)+sqr(t.y));
z.x := 2/3*t.x + (sqr(t.x)-sqr(t.y))/(3*p);
z.y := 2/3*t.y*(1-t.x/p);{}
d.x := abs(t.x - z.x);
d.y := abs(t.y - z.y);
Inc(n);
end;
col := (n*9) mod 255;
PaintBox1.Canvas.Pixels[mx+x,my+y]:=RGBTOColor(col,0,col);
end;
end;
end.| Прикрепленный файл | Размер |
|---|---|
| Исходные коды и исполняемый файл | 763.67 кб |
grafika.me