Элементы комбинаторики
Правило сложения
Правило сложения используется в том случае, если у нас есть два или более множеств, которые попарно не пересекаются, то есть не имеют общих элементов. И нам нужно найти сколько элементов содержится в объединении этих множеств. В этом случае мы складываем число элементов в каждом множестве. Простейший пример: если у нас есть две корзинки с фруктами: в одной 5 яблок, а в другой 7 груш. Если мы эти фрукты пересыпаем в одну корзинку (объединяем множества), тогда в новой корзинке окажется 5+7=12 фруктов.
Правило умножения
Правило умножения используется в том случае, если у нас есть два множества, и мы составляем всевозможные пары из элементов этих множеств. Например, если взять множество, состоящее из 5-ти яблок и множество, состоящее из 7-ми груш и составить всевозможные пары из этих фруктов, то мы получим всевозможных пар.
Действительно. Возьмем первое яблоко. Мы можем положить к нему любую из семи груш, то есть получаем 7 пар. Возьмем второе яблоко, и к нему мы также можем положить любую из 7-ми груш, получаем ещё 7 пар. И так далее. Всего получается пар.
Правило умножения легко понять, если попытаться ответить, например, на такой вопрос: «сколько существует двузначных чисел?«
Пусть двузначное чиcло имеет вид , где — число десятков, — число единиц. При этом цифра может принимать значения от 1 до 9 ( цифра 0 не может стоять на первом месте, так как в этом случаем мы получим однозначное число), цифра может принимать значения от 0 до 9.
Пусть , и у нас есть 10 вариантов цифр, которые могут стоять на втором месте. Тогда мы имеем 10 двузначных чисел, содержащих 1 десяток.
Затем мы берем и так же получаем 10 двузначных чисел, у которых теперь уже 2 десятка.
И так далее.
Так как цифра может принимать 9 различных значений, то получаем двузначных чисел.
Зная, что на первом месте может стоять 9 различных цифр, а на втором — 10, мы получаем комбинаций этих цифр, то есть все возможные двузначные числа. Здесь важно понимать, что любая цифра, стоящая на первом месте, может сочетаться с любой цифрой, стоящей на втором месте.
В общем случае правило умножения звучит так:
Если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару (A, B) можно выбрать n·m способами. Это правило распространяется на любое число независимо выбираемых элементов.
Если мы хотим ответить на вопрос, сколько существует трехзначных чисел, мы заметим, что в трехзначном числе первая цифра может принимать 9 значений, вторая — 10, и третья — 10 значений. И мы получаем трехзначных чисел.
Формула включений-исключений
используется в том случае, если нам нужно найти число элементов в объединении двух множеств, в том случае, если эти множества пересекаются.
Пусть множество А содержит n элементов, множество В содержит m элементов, и пересечение этих множеств содержит k элементов. То есть k элементов содержатся и в множестве А, и в множестве В. Тогда объединение множеств содержит m+n-k элементов.
Действительно, при объединении двух множеств мы k элементов посчитали два раза, и теперь один раз мы должны их вычесть.
Число элементов в множестве обозначается общепринятым значком #. Тогда формула для подсчета числа элементов в объединении трех множеств имеет вид:
########
Рассмотрим примеры задач.
1. Сколько трехзначных чисел содержит хотя бы одну цифру 3?
Решение.
показать
2. Сколько четырехзначных чисел, кратных 5.
Решение.
показать
Перестановки
Воспользуемся правилом умножения чтобы ответить на вопрос, «сколькими способами можно построить 7 человек в шеренгу?».
Человека, стоящего первым в шеренге можно выбрать семью способами, второго можно выбрать из оставшихся шести человек, то есть шестью способами. Третьего, соответственно, пятью. И так далее. Последнего можно выбрать единственным способом. Всего получаем способов построить 7 человек в шеренгу.
В общем случае, если мы имеем объектов, которые хотим расположить в определенном порядке (пронумеровать их), то мы получим
способов расположения этих объектов.
Факториалом натурального числа называется произведение всех натуральных чисел от 1 до :
По определению 0!=1; 1!=1.
Перестановкой из предметов называется любой способ нумерации этих предметов (способ расположения их в ряд).
Число перестановок предметов равно .
3. Имеется 10 компьютерных дисков и 10 коробок от них. Найдите вероятность того, что случайным образом уложив диски в коробки, мы обнаружим, что
1. Каждый диск лежит в своей коробке.
2. Хотя бы один диск лежит не в своей коробке.
3. Два определенных диска перепутаны местами, а остальные в своих коробках.
4. Ровно один лежит не в своей коробке, а остальные — в своих коробках.
Решение.
показать
1. Пронумеруем диски и коробки. Расположим коробки в определенной последовательности. Нам нужно, чтобы при случайном расположении дисков в ряд, их номера тоже оказались расположены в той же последовательности.
Расположить 10 чисел в определенной последовательности можно единственным способом, то есть мы имеем 1 благоприятный исход.
Расположить 10 чисел в произвольном порядке можно 10! способами.
Следовательно, вероятность того, что каждый диск окажется в своей коробке равна
2. Событие «хотя бы один диск лежит не в свой коробке» противоположно событию «каждый диск лежит в своей коробке«, и его вероятность равна
3. Событие «два определенных диска перепутаны местами, а остальные в своих коробках», также как событие «каждый диск лежит в своей коробке«, имеет единственный благоприятный исход, поэтому вероятность этого события равна
4. Событие «ровно один лежит не в своей коробке, а остальные — в своих коробках» невозможно, так как если один диск лежит не своей коробке, то обязательно должен найтись ещё один, который так же лежит не в своей коробке. Поэтому вероятность этого события равна нулю.
4. Слово «МАТЕМАТИКА» написали на полоске картона и разрезали полоску на буквы. Найдите вероятность того, что составив все эти буквы случайным образом в ряд, мы снова получим слово «МАТЕМАТИКА».
Сколько буквосочетаний можно составить из букв слова «МАТЕМАТИКА»?
Решение.
показать
1 способ.
Вероятность того, что на первом месте будет стоять буква М равна 2/10 — у нас две буквы М, и всего 10 букв.
Вероятность того, что на втором месте будет стоять буква А равна 3/9 — у нас осталось 9 букв, из которых 3 буквы А.
Вероятность того, что на втором месте будет стоять буква Т равна 2/8 — у нас осталось 8 букв, из которых 2 буквы Т.
И так далее. В итоге получаем:
2 способ.
Пронумеруем все буквы в слове «МАТЕМАТИКА». Найдем, сколькими способами мы можем их расположить в определенном порядке. В слове 10 букв, и мы можем их расположить 10!=3628800 различными способами.
Поскольку в слове есть одинаковые буквы, то при перестановке этих букв мы получим то же слово:
в слове «МАТЕМАТИКА» 2 буквы «М»; 3 буквы «А»; 2 буквы «Т», следовательно по правилу произведения это дает нам способов перестановки этих букв с сохранением слова «МАТЕМАТИКА».
Таким образом, вероятность снова получить слово «МАТЕМАТИКА» равна:
Сколько буквосочетаний можно составить из букв слова «МАТЕМАТИКА»?
Из 10 букв слова «МАТЕМАТИКА» можно составить 10! буквосочетаний. Но некоторые из них будут одинаковыми, так как при перестановке одинаковых букв, мы будем получать те же буквосочетания. То есть в итоге мы получим
буквосочетаний.
Размещения
В задачах по теории вероятностей часто возникает необходимость определить, сколькими способами можно выбрать определенное число предметов и расположить их в определенном порядке.
5. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?
Воспользуемся правилом умножения.
В первую страну мы выбираем из 9 специалистов, то есть у нас 9 вариантов выбора. После того, как специалист для поездки в первую страну выбран, у нас осталось 8 специалистов, и для поездки во вторую страну у нас 8 вариантов выбора. И так далее… в четвертую страну мы можем выбрать кандидата из 6 специалистов.
Таким образом, мы получаем вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны.
Обобщим эту задачу на случай выбора k кандидатур из n специалистов для поездки в k различных стран.
Рассуждая аналогичным образом, мы получаем
вариантов.
Если умножить и разделить это выражение на , то получим следующую формулу:
В этой задаче из множества, состоящего из элементов мы выбрали упорядоченные подмножества (для нас был важен порядок расположения элементов в подмножестве), состоящие из элементов. Задача сводилась к нахождению числа таких подмножеств.
Такие упорядоченные подмножества называются размещениями из n элементов по k.
Пусть у нас есть множество , состоящее из элементов. Размещением (из n по k) называется упорядоченное подмножество из различных элементов из некоторого множества , состоящего из различных элементов.
Число размещений из элементов по обозначается и находится по формуле:
Размещения с повторениями
6. Игральную кость бросают трижды. Сколько различных комбинаций выпавших очков при этом получится?
При бросании кости первый раз мы получим 6 различных вариантов: 1 очко, 2, 3… или 6. Аналогично при бросании кости во второй и в третий раз мы получим также по 6 различных вариантов. По правилу умножения получим число различных комбинаций трех чисел, принимающих значения от 1 до 6:
В общем случае:
Пусть у нас есть множество , состоящее из элементов.
Любой упорядоченный набор элементов множества, состоящего из элементов называется размещением с повторением из элементов по . Число различных размещений с повторениями равно
.
Действительно. Представим ящик с пронумерованными шарами. Мы вынимаем шар, записываем его номер и возвращаем обратно, и так раз. Сколько комбинаций из номеров мы можем получить?
Поскольку шары каждый раз возвращаются, каждый раз, вынимая шар из коробки, в которой шаров, мы можем получить различных чисел. По правилу умножения имеем
Сочетания
Рассмотрим задачу, аналогичную задаче 5, но с существенным отличием.
7. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов?
В этой задаче нам нужно выбрать 4 кандидатуры, но при этом не важно, в каком порядке мы их выбираем, нас интересует только состав выбранных элементов, но не порядок их расположения.
Если бы нас интересовал порядок расположения элементов, как в задаче 5, то мы могли применили бы формулу для нахождения числа размещений из 9 по 4:
4 различных элемента можно расположить в определенном порядке 4! различными способами. Поскольку нас не интересует порядок расположения элементов, число способов, которыми мы можем выбрать 4 элемента, не располагая их в определенном порядке, уменьшается в 4! раза по сравнению с предыдущей задачей (так как для данной задачи различное расположение данных элементов считается одним способом), и мы получаем
способов.
В этой задаче появляется понятие сочетания.
Сочетаниями из n элементов по k элементов называются подмножества, состоящие из k элементов множества (множества, состоящего из n элементов).
Внимание! Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).
Число сочетаний из n элементов по k элементов обозначается
и находится по формуле:
Число сочетаний из n по k показывает, сколькими способами мы можем выбрать k элементов из n элементов, или сколькими способами мы можем расположить k объектов по n местам.
Легко заметить, что
8. В коробке лежат 8 красных карандашей и 4 синих. Из коробки наугад вынимают 4 карандаша. Какова вероятность того, что среди них окажется 2 красных и 2 синих?
Решение.
показать
Всего в коробке 12 карандашей. Найдем, сколькими способами способами можно извлечь из коробки 4 карандаша. Так как нас не интересует порядок, в котором карандаши извлекаются из коробки, а только состав карандашей, это число равно числу сочетаний из 12 по 4:
Из 8 красных карандашей можно извлечь два карандаша способами.
Из 4 синих карандашей можно извлечь два карандаша способами.
По правилу произведения получаем, что извлечь 2 синих и 2 красных карандаша можно способами.
Таким образом, искомая вероятность равна:
Метод шаров и перегородок
9. Сколькими способами можно разложить 10 шаров в 4 коробки? Предполагается, что некоторые коробки могут оказаться пустыми.
Решение.
Рассмотрим 10 шаров:
Будем «раскладывать шары по коробкам», ставя перегородки.
Например, так:
В этом примере в первой коробке 3 шара, во второй — 2, в третьей — 4, и в четвертой — 2. Переставляя шары и перегородки, мы получаем различные комбинации шаров в коробках. Например, переставив последний шар в первой коробке и первую внутреннюю перегородку, мы получим такую комбинацию:
Таким образом, мы получаем различное число шаров в коробках, комбинируя позиции 10-ти шаров и 3-х внутренних перегородок. Чтобы определить, сколько различных комбинаций мы можем получить, нам нужно найти число сочетаний из 13 по 3. (Или, что то же самое, что число сочетаний из 13 по 10.) Столько способов выбрать 3 места для перегородок из 13 возможных позиций. Или, что то же самое, 10 мест для шаров.
10. Сколько решений имеет уравнение в целых неотрицательных числах?
Решение.
Так как переменные могут принимать только целые неотрицательные значения, следовательно, у нас есть 10 переменных, и они могут принимать значения 0, 1, 2, 3 и 4. Представим, что у нас есть 10 коробок (это переменные), и мы должны разложить по этим коробкам 4 шара. Сколько шаров попадет в коробку, таково значение соответствующей переменной. Если у нас 10 коробок, следовательно, 10-1=9 внутренних перегородки. И 4 шара. Всего 13 мест. Нам надо расположить на этих 13 местах 4 шара. Число таких возможностей:
В общем случае, если нам нужно разложить шаров в коробок, мы получаем комбинации из шаров и внутренней перегородки. И число таких комбинаций равно числу сочетаний из по .
В этой задаче мы имели дело с сочетаниями с повторениями.
Сочетания с повторениями
Сочетаниями из элементов по элементов с повторениями называются группы, содержащие элементов, причем каждый элемент принадлежит к одному из типов.
Что такое сочетания из элементов по элементов с повторениями можно понять с помощью такого мысленного эксперимента. Представим ящик с пронумерованными шарами. Мы вынимаем шар, записываем его номер и возвращаем обратно, и так раз. В отличие от размещений с повторениями нас не интересует порядок записанных чисел, а только их состав. Например, группы чисел {1,1,2,1,3,1,2} и {1,1,1,1,2,2,3} считаются одинаковыми. Сколько таких групп из номеров мы можем получить?
В конечном итоге нас интересует сколько элементов каждого типа (всего n типов элементов) содержится в каждой группе (из k элементов), и сколько таких различных вариантов может быть. То есть мы находим, сколько в целых неотрицательных решений имеет уравнение уравнение — задача аналогична задаче по раскладыванию n шаров в k коробок.
Число сочетаний с повторениями находится по такой формуле:
Таким образом, число сочетаний с повторениями — это количество способов представить число k в виде суммы n слагаемых.
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Метод шаров и перегородок — Википедия
Метод шаров и перегородок (англ. stars and bars — букв. «звёздочки и чёрточки») — это графический метод для вывода некоторых комбинаторных теорем. Метод популяризировал Уильям Феллер в его классической книге по теории вероятностей. Метод может быть использован для решения многих простых задач подсчёта, таких как «сколькими способами можно разложить n неразличимых шаров по k различимым ящикам»[1][2].
Метод шаров и перегородок часто представляется доказательством следующих двух теорем элементарной комбинаторики.
Теорема 1[править | править код]
Для любой пары натуральных чисел n и k число k-кортежей натуральных чисел, сумма которых равна n, равно числу (k−1){\displaystyle (k-1)}-элементных подмножеств множества из n−1{\displaystyle n-1} элементов.
Оба эти числа задаются биномиальным коэффициентом (n−1k−1){\displaystyle \textstyle {n-1 \choose k-1}}. Например, при n = 3 и k = 2 кортежи, подсчитанные теоремой, это (2, 1) и (1, 2), и существует (3−12−1)=2{\displaystyle {\tbinom {3-1}{2-1}}=2} таких кортежей.
Теорема 2[править | править код]
Для любой пары натуральных чисел n и k число k-кортежей неотрицательных целых чисел, сумма которых равна n, равно числу мультимножеств мощности k – 1, взятых из множества размера n + 1.
Оба числа равны числу мультимножеств ((n+1k−1)){\displaystyle \left(\!{\tbinom {n+1}{k-1}}\!\right)}, или, эквивалентно, биномиальному коэффициенту (n+k−1k−1)=(n+k−1n){\displaystyle {\tbinom {n+k-1}{k-1}}={\tbinom {n+k-1}{n}}} или числу мультимножеств ((kn)){\displaystyle {\big (}\!{\tbinom {k}{n}}\!{\big )}}. Например, при n = 3 и k = 2 кортежи, подсчитываемые теоремой, — это (3, 0), (2, 1), (1, 2) и (0, 3), и имеется ((3+12−1))=4{\displaystyle \left(\!{\tbinom {3+1}{2-1}}\!\right)=4} таких кортежей.
Доказательства с помощью шаров и перегородок[править | править код]
Теорема 1[править | править код]
Предположим, что имеется n объектов (которые представляются шарами, В примере ниже n = 7) нужно разместить в k ящиках (в примере k = 3) таким образом, что все ящики должны содержать по меньшей мере один объект. Ящики различаются (скажем, они пронумерованы числами 1 от k), но шары неразличимы (так что конфигурации различимы по числу шаров, находящихся в каждом ящике, фактически, конфигурация представляет k-кортеж положительных чисел, как в утверждении теоремы). Вместо размещения шаров в ящиках шары располагаются в линию:
● ● ● ● ● ● ●
Рис. 1: семь объектов, представленных шарами
где шары для первого ящика берутся слева, затем идут шары второго ящика и так далее. Таким образом, конфигурация определяется тем, какой начальный шар принадлежит первому ящику, какой первый (самый левый) шар принадлежит второму ящику и так далее. Можно отмечать это положение, помещая k − 1 разделяющих перегородок в некоторых местах между двумя шарами; а поскольку никакой ящик не может оказаться пустым, между двумя соседними шарами может быть не более одной перегородки:
| ● ● ● ● | | | ● | | | ● ● |
Рис. 2: две перегородки задают три ящика, содержащие 4, 1 и 2 объектов
Тогда n шаров как фиксированные объекты определяют n − 1 промежутков между шарами, в каждый из которых можно поместить (или не поместить) одну перегородку. Нужно выбрать k − 1 мест, в которых разместить перегородки, поэтому имеется (n−1k−1){\displaystyle {\tbinom {n-1}{k-1}}} возможных конфигураций (см. Сочетание).
Теорема 2[править | править код]
В этом случае представление кортежей как последовательности шаров и перегородок остаётся неизменным. Накладываемое более слабое условие неотрицательности (вместо положительности) означает, что можно расположить несколько перегородок между двумя шарами, а также можно располагать перегородки перед первым шаром и после последнего. Таким образом, например, при n = 7 и k = 5 кортеж (4, 0, 1, 2, 0) может быть представлен следующим рисунком.
| ● ● ● ● | | | | | ● | | | ● ● | | |
Рис. 3: четыре перегородки образуют пять ящиков, содержащих 4, 0, 1, 2 и 0 объектов
Это устанавливает соответствие один-к-одному между кортежами такого вида и выборками с возвращением k − 1 промежутков среди n + 1 возможных промежутков, или, эквивалентно, (k − 1)-элементных мультимножеств, взятых из множества размера n + 1. По определению, такие объекты подсчитываются числом мультивыбора ((n+1k−1)){\displaystyle \left(\!{\tbinom {n+1}{k-1}}\!\right)}.
Чтобы видеть, что те же объекты подсчитываются биномиальным коэффициентом (n+k−1n){\displaystyle {\tbinom {n+k-1}{n}}}, заметим, что желаемое расположение состоит из n + k − 1 объектов (n шаров и k − 1 перегородок). Выбор позиций для шаров оставляет ровно k − 1 мест для k − 1 перегородок. То есть выбор позиций для шаров определяет всю конфигурацию, так что число конфигураций равно (n+k−1n){\displaystyle {\tbinom {n+k-1}{n}}}. Заметим, что (n+k−1n)=(n+k−1k−1){\displaystyle {\tbinom {n+k-1}{n}}={\tbinom {n+k-1}{k-1}}}, что отражает факт, что конфигурация определяется выбором позиций для k − 1 перегородок.
Если n = 5, k = 4 и множество размера k — {a, b, c, d}, то ●|●●●||● представляет мультимножество {a, b, b, b, d} или 4-кортеж (1, 3, 0, 1). Представление любого мультимножества для этого примера будет использовать n = 5 шаров и k − 1 = 3 перегородок.
Многие элементарные задачи в комбинаторике решаются вышеприведёнными теоремами. Например, если нужно подсчитать число способов распределить семь неразличимых десятирублёвых монет между Анной, Борисом и Виталием так, что каждый из них получит по меньшей одну монету, можно заметить, что распределение эквивалентно кортежу из трёх натуральных чисел, сумма которых равна 7. (Здесь первая позиция в кортеже определяет число монет, отдаваемых Анне, и так далее.) Таким образом, метод шаров и перегородок применим с n = 7 и k = 3, что даёт (7−13−1)=15{\displaystyle \textstyle {7-1 \choose 3-1}=15} способов распределения монет.
- Feller W. An Introduction to Probability Theory and Its Applications. — 2nd ed.. — Wiley, 1950. — Т. 1.
- Феллер В. Введение в теорию вероятностей и её приложения. — М.: Мир, 1984. — Т. 1.
- Jim Pitman. Probability. — Berlin: Springer-Verlag, 1993. — ISBN 0-387-97974-3.
- Weisstein, Eric W. Multichoose (неопр.). Mathworld — A Wolfram Web Resource. Проверено 18 ноября 2012.
ru.wikiyy.com
Метод шаров и перегородок Википедия
Метод шаров и перегородок (англ. stars and bars — букв. «звёздочки и чёрточки») — это графический метод для вывода некоторых комбинаторных теорем. Метод популяризировал Уильям Феллер в его классической книге по теории вероятностей. Метод может быть использован для решения многих простых задач подсчёта, таких как «сколькими способами можно разложить n неразличимых шаров по k различимым ящикам»[1][2].
Утверждения теорем[ | ]
Метод шаров и перегородок часто представляется доказательством следующих двух теорем элементарной комбинаторики.
Теорема 1[ | ]
Для любой пары натуральных чисел n и k число k-кортежей натуральных чисел, сумма которых равна n, равно числу (k−1){\displaystyle (k-1)}-элементных подмножеств множества из n−1{\displaystyle n-1} элементов.
Оба эти числа задаются биномиальным коэффициентом (n−1k−1){\displaystyle \textstyle {n-1 \choose k-1}}. Например, при n = 3 и k = 2 кортежи, подсчитанные теоремой, это (2, 1) и (1, 2), и существует (3−12−1)=2{\displaystyle {\tbinom {3-1}{2-1}}=2} таких кортежей.
Теорема 2[ | ]
Для любой пары натуральных чисел n и k число k-кортежей неотрицательных целых чисел, сумма которых равна n, равно числу мультимножеств мощности k – 1, взятых из множества размера n + 1.
Оба числа равны числу мультимножеств ((n+1k−1)){\displaystyle \left(\!{\tbinom {n+1}{k-1}}\!\right)}, или, эквивалентно, биномиальному коэффициенту
ru-wiki.ru
Метод шаров и перегородок Википедия
Метод шаров и перегородок (англ. stars and bars — букв. «звёздочки и чёрточки») — это графический метод для вывода некоторых комбинаторных теорем. Метод популяризировал Уильям Феллер в его классической книге по теории вероятностей. Метод может быть использован для решения многих простых задач подсчёта, таких как «сколькими способами можно разложить n неразличимых шаров по k различимым ящикам»[1][2].
Утверждения теорем
Метод шаров и перегородок часто представляется доказательством следующих двух теорем элементарной комбинаторики.
Теорема 1
Для любой пары натуральных чисел n и k число k-кортежей натуральных чисел, сумма которых равна n, равно числу (k−1){\displaystyle (k-1)}-элементных подмножеств множества из n−1{\displaystyle n-1} элементов.
Оба эти числа задаются биномиальным коэффициентом (n−1k−1){\displaystyle \textstyle {n-1 \choose k-1}}. Например, при n = 3 и k = 2 кортежи, подсчитанные теоремой, это (2, 1) и (1, 2), и существует (3−12−1)=2{\displaystyle {\tbinom {3-1}{2-1}}=2} таких кортежей.
Теорема 2
Для любой пары натуральных чисел n и k число k-кортежей неотрицательных целых чисел, сумма которых равна n, равно числу мультимножеств мощности k – 1, взятых из множества размера n + 1.
Оба числа равны числу мультимножеств ((n+1k−1)){\displaystyle \left(\!{\tbinom {n+1}{k-1}}\!\right)}, или, эквивалентно, биномиальному коэффициенту (n+k−1k−1)=(n+k−1n){\displaystyle {\tbinom {n+k-1}{k-1}}={\tbinom {n+k-1}{n}}} или числу мультимножеств ((kn)){\displaystyle {\big (}\!{\tbinom {k}{n}}\!{\big )}}. Например, при n = 3 и k = 2 кортежи, подсчитываемые теоремой, — это (3, 0), (2, 1), (1, 2) и (0, 3), и имеется ((3+12−1))=4{\displaystyle \left(\!{\tbinom {3+1}{2-1}}\!\right)=4} таких кортежей.
Доказательства с помощью шаров и перегородок
Теорема 1
Предположим, что имеется n объектов (которые представляются шарами, В примере ниже n = 7) нужно разместить в k ящиках (в примере k = 3) таким образом, что все ящики должны содержать по меньшей мере один объект. Ящики различаются (скажем, они пронумерованы числами 1 от k), но шары неразличимы (так что конфигурации различимы по числу шаров, находящихся в каждом ящике, фактически, конфигурация представляет k-кортеж положительных чисел, как в утверждении теоремы). Вместо размещения шаров в ящиках шары располагаются в линию:
● ● ● ● ● ● ●
Рис. 1: семь объектов, представленных шарами
где шары для первого ящика берутся слева, затем идут шары второго ящика и так далее. Таким образом, конфигурация определяется тем, какой начальный шар принадлежит первому ящику, какой первый (самый левый) шар принадлежит второму ящику и так далее. Можно отмечать это положение, помещая k − 1 разделяющих перегородок в некоторых местах между двумя шарами; а поскольку никакой ящик не может оказаться пустым, между двумя соседними шарами может быть не более одной перегородки:
| ● ● ● ● | | | ● | | | ● ● |
Рис. 2: две перегородки задают три ящика, содержащие 4, 1 и 2 объектов
Тогда n шаров как фиксированные объекты определяют n − 1 промежутков между шарами, в каждый из которых можно поместить (или не поместить) одну перегородку. Нужно выбрать k − 1 мест, в которых разместить перегородки, поэтому имеется (n−1k−1){\displaystyle {\tbinom {n-1}{k-1}}} возможных конфигураций (см. Сочетание).
Теорема 2
В этом случае представление кортежей как последовательности шаров и перегородок остаётся неизменным. Накладываемое более слабое условие неотрицательности (вместо положительности) означает, что можно расположить несколько перегородок между двумя шарами, а также можно располагать перегородки перед первым шаром и после последнего. Таким образом, например, при n = 7 и k = 5 кортеж (4, 0, 1, 2, 0) может быть представлен следующим рисунком.
| ● ● ● ● | | | | | ● | | | ● ● | | |
Рис. 3: четыре перегородки образуют пять ящиков, содержащих 4, 0, 1, 2 и 0 объектов
Это устанавливает соответствие один-к-одному между кортежами такого вида и выборками с возвращением k − 1 промежутков среди n + 1 возможных промежутков, или, эквивалентно, (k − 1)-элементных мультимножеств, взятых из множества размера n + 1. По определению, такие объекты подсчитываются числом мультивыбора ((n+1k−1)){\displaystyle \left(\!{\tbinom {n+1}{k-1}}\!\right)}.
Чтобы видеть, что те же объекты подсчитываются биномиальным коэффициентом (n+k−1n){\displaystyle {\tbinom {n+k-1}{n}}}, заметим, что желаемое расположение состоит из n + k − 1 объектов (n шаров и k − 1 перегородок). Выбор позиций для шаров оставляет ровно k − 1 мест для k − 1 перегородок. То есть выбор позиций для шаров определяет всю конфигурацию, так что число конфигураций равно (n+k−1n){\displaystyle {\tbinom {n+k-1}{n}}}. Заметим, что (n+k−1n)=(n+k−1k−1){\displaystyle {\tbinom {n+k-1}{n}}={\tbinom {n+k-1}{k-1}}}, что отражает факт, что конфигурация определяется выбором позиций для k − 1 перегородок.
Примеры
Если n = 5, k = 4 и множество размера k — {a, b, c, d}, то ●|●●●||● представляет мультимножество {a, b, b, b, d} или 4-кортеж (1, 3, 0, 1). Представление любого мультимножества для этого примера будет использовать n = 5 шаров и k − 1 = 3 перегородок.
Многие элементарные задачи в комбинаторике решаются вышеприведёнными теоремами. Например, если нужно подсчитать число способов распределить семь неразличимых десятирублёвых монет между Анной, Борисом и Виталием так, что каждый из них получит по меньшей одну монету, можно заметить, что распределение эквивалентно кортежу из трёх натуральных чисел, сумма которых равна 7. (Здесь первая позиция в кортеже определяет число монет, отдаваемых Анне, и так далее.) Таким образом, метод шаров и перегородок применим с n = 7 и k = 3, что даёт (7−13−1)=15{\displaystyle \textstyle {7-1 \choose 3-1}=15} способов распределения монет.
См. также
Примечания
Литература
- Feller W. An Introduction to Probability Theory and Its Applications. — 2nd ed.. — Wiley, 1950. — Т. 1.
- Феллер В. Введение в теорию вероятностей и её приложения. — М.: Мир, 1984. — Т. 1.
- Jim Pitman. Probability. — Berlin: Springer-Verlag, 1993. — ISBN 0-387-97974-3.
Ссылки
- Weisstein, Eric W. Multichoose (неопр.). Mathworld — A Wolfram Web Resource. Проверено 18 ноября 2012.
wikiredia.ru
Шары и перегородки
Documents войти Загрузить ×- Математика
Related documents

Соответствие и исключение
счастливого» билета

Задания олимпиады 21.02.2015 для 9 классов

Самое трудное – научить любого ребенка пользоваться

Уравнения в целых числах

Домашнее задание 8 класс

Задачи заочного тура Олимпиады ТГТУ-2015

М39

204* Найти два натуральных числа, сумма и произведение ко

Учитель Зинатуллина Л.Т. МБОУ «Ципьинская СОШ» Разработка урока

Счастливые люди…

Нестандартные задачи по математике в первом классе

Соответствие и исключение

Задачи_малышковой_информатика
Повышение качества жизни
studydoc.ru
СТЕНА ИЗ ШАРОВ — Мастер-классы
Для стены из шаров нам понадобятся:
— каркас
— прочная веревка (на 4 кв.метра примерно 20 метров веревки)
— 300 шаров разного размера (для стены из шаров 4 кв.метра)
— насос
Для изготовления стены из шаров в помещении идеально подошел бы каркас в виде джокерной конструкции. Но при уличном изготовлении такой вариант не подойдет,потому что из-за порыва ветра вся композиция может завалиться,будет неустойчива.
Мы в качетсве каркаса взяли два столба на расстоянии 2 метра друг от друга. Столбы вкопаны в землю. (деревья тоже подойдут)
К одному из стобов привязали веревку и обернули наши каркасные столбы веревкой на расстоянии примерно 30 см между оборотами

Теперь, когда каркас готов, приступим к, собственно, изготовлению стены из шаров.
Для этого надуем и свяжем попарно (по 2 шт) все 300 шаров. Для этого можно использовать пылесос с функцией выдувания.

После того, как шары надули, начинаем монтировать стену. Для этого, начиная с верхнего угла привязываем к натянутой веревке по 2, по 4 шара в хаотичном порядке,заполняя постепенно всю стену сверху вниз

В зазоры, образовавшиеся между рядами, привязываем одиночные шары.
В результате у вас должна получиться такая стена

На свежем воздухе, на свету шары станут матовыми.
Купите фольгированную цифру, надуйте ее воздухом и у вас получится великолепное украшение из шаров, которое также является фоном для фотографий

Если при надувании шаров, вы засунете в пару-тройку шаров записку или конфетку, то демонтаж стены можно превратить в веселый конкурс «Найди записку — получишь приз». Дети с радостью полопают все шарики за считанные минуты.

Надеемся, что наш мастер-класс окажется полезным для вас.
ukrasharik.ru
Как украсить стены шарами и лентами

Я очень люблю простые и эффектные приемы оформления из доступных материалов. Именно такое украшение я сегодня добавляю в свою коллекцию праздничных идей.
Как выглядит тучка
Шары одного или нескольких цветов собраны в длинное облачко. Для крепления используется жесткая планка или палочка. Длина украшения может быть от 1 до 3 метров.
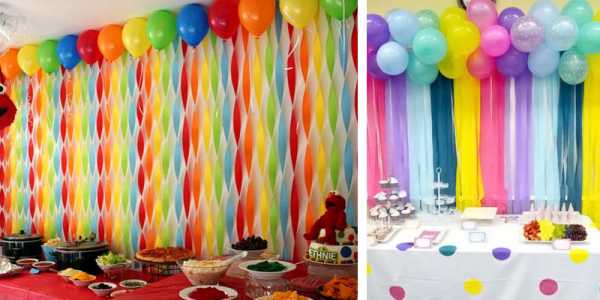
По всей длине на планку крепятся яркие ленты. Это могут быть полоски из гофрированной бумаги (продаются готовые в интернет-магазинах) или самые обычные атласные ленты.
Ленты могут спускаться до пола, но, если украшение служит фоном для сладкого стола (candy bar), имеет смысл протянуть полоски до столешницы. Мне нравятся скрученные ленты — добавляется объем и игра света и тени. Очень празднично!
Вместо лент часто используют готовые вертикальные гирлянды. Вы можете сделать дождик не только из бумажных капель, но и из сердечек, звездочек, бабочек и разноцветных кружочков. Магазины с праздничными товарами предлагают огромный выбор, самим ничего клеить не нужно.

Удивительно, но фотозону можно сделать из одних только лент, нанизанных на тесьму. Даже без шаров такой декор выглядит эффектно.

Вместо латентных шаров можно сделать тучку из бумажных шаров, ананасов и яблочек. В сочетании с искусственными пальмовыми ветвями получается очень по-летнему! Это быстрое и эффектное настенное украшение для детского праздника. На взрослом юбилее так оформляют фотозоны и делают фон для candy bar.
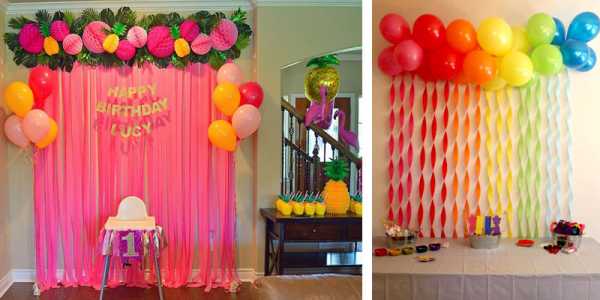
Лаконичную цветовую гамму выбирают для оформления мальчиковых праздников. Кстати, если вы создадите черно-белую тучку с черно-белыми лентами, получите замечательную фотозону и для мужского праздника.

Если вы не плетете плотную симметричную гирлянду в качестве тучки, используйте много шаров разного размера и свяжите их в пышные пучки, иначе смотрится грустновато.

Тучка может располагаться не только на стене, но и на потолке. Несколько десятков ярких лет помогут вам скрыть недостатки потолка.

Стоимость изготовления такого украшения зависит от количества шаров, сложности монтажа, количества и качества лент. Если в «тучку» будут добавлены бумажные шары, звезды, кисточки или искусственные цветы, стоимость увеличится.
Ирина Панасьян
snova-prazdnik.ru
